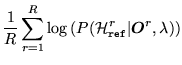 |
|||
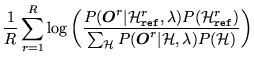 |
(8.8) |
The previous sections have described how maximum likelihood (ML)-based estimates of the HMM model parameters can be initialised and estimated. This section briefly describes how discriminative training is implemented in HTK. It is not meant as a definitive guide to discriminative training, it aims to give sufficient information so that the configuration and command-line options associated with the discriminative training tool HMMIREST can be understood.
HTK supports discriminative training using the HMMIREST tool. The use
of both the Maximum Mutual Information (MMI) and Minimum
Phone Error (MPE) training criteria are supported. In both cases the aim is
to estimate the HMM parameters in such a way as to (approximately) reduce the
error rate on the training data. Hence the criteria take into account not
only the actual word-level transcription of the training data but also
``confusable'' hypotheses which give rise to similar language model / acoustic
model log likelihoods. The form of MMI criterion to be maximised may be
expressed as 8.1
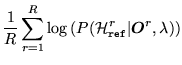 |
|||
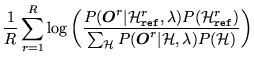 |
(8.8) |
The MPE training criterion is an example of minimum Bayes' risk
training8.2. The general
expression to be minimised can be expressed as
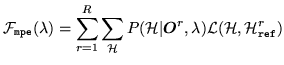 |
(8.9) |
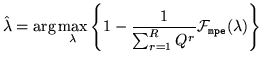 |
(8.10) |
In the HMMIREST implementation the language model scores, including
the grammar scale factor are combined into the acoustic models to yield a
numerator acoustic model,
![]() , and a denominator acoustic
model,
, and a denominator acoustic
model,
![]() for utterance
for utterance ![]() . In this case the MMI criterion can be expressed as
. In this case the MMI criterion can be expressed as
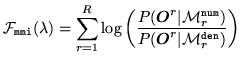 |
(8.11) |
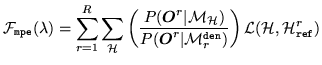 |
(8.12) |
In practice approximate forms of the MMI and normalised average phone accuracy criteria are optimised.