For both MMI and MPE training the estimation of the model parameters are based
on variants of the Extended Baum-Welch (EBW) algorithm. In HTK the following
form is used to estimate the means and covariance matrices8.3
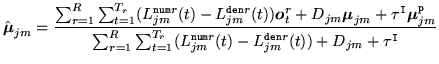 |
|
|
(8.13) |
and
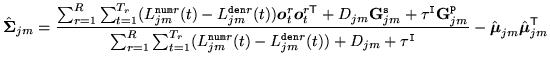 |
|
|
(8.14) |
where
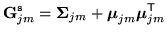 |
|
|
(8.15) |
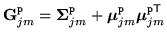 |
|
|
(8.16) |
The difference between the MMI and MPE criteria lie in how the numerator,
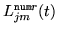 , and denominator,
, and denominator,
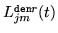 ,
``occupancy probabilities'' are computed. For MMI, these are the posterior
probabilities of Gaussian component occupation for either the numerator or denominator lattice. However for MPE, in order to keep the same form of re-estimation
formulae as MMI, an MPE-based analogue of the ``occupation
probability'' is computed which is related to an approximate error
measure for each phone marked for the denominator: the
positive values are treated as numerator statistics and negative
values as denominator statistics.
,
``occupancy probabilities'' are computed. For MMI, these are the posterior
probabilities of Gaussian component occupation for either the numerator or denominator lattice. However for MPE, in order to keep the same form of re-estimation
formulae as MMI, an MPE-based analogue of the ``occupation
probability'' is computed which is related to an approximate error
measure for each phone marked for the denominator: the
positive values are treated as numerator statistics and negative
values as denominator statistics.
In these update formulae there are a
number of parameters to be set.
- Smoothing constant,
 : this is a state-component specific
parameter that determines the contribution of the counts from the current
model parameter estimates. In HMMIREST this is set at
: this is a state-component specific
parameter that determines the contribution of the counts from the current
model parameter estimates. In HMMIREST this is set at
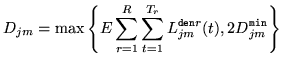 |
|
|
(8.17) |
where
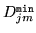 is the minimum value of
is the minimum value of  to ensure that
to ensure that
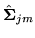 is positive semi-definite.
is positive semi-definite. 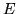 is specified using the
configuration variable E.
is specified using the
configuration variable E.
- I-smoothing constant,
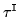 : global smoothing term to improve
generalisation by using the state-component priors,
: global smoothing term to improve
generalisation by using the state-component priors,
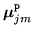 and
and
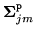 . This is set using the configuration option
ISMOOTHTAU.
. This is set using the configuration option
ISMOOTHTAU.
- Prior parameters,
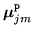 and
and
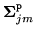 : the prior parameters that the counts from the training data are smoothed with. These may be
obtained from a number of sources. Supported options are;
: the prior parameters that the counts from the training data are smoothed with. These may be
obtained from a number of sources. Supported options are;
- dynamic ML-estimates (default): the ML estimates of the mean and
covariance matrices, given the current model parameters, are used.
- dynamic MMI-estimates: for MPE training the MMI estimates of the mean and
covariance matrices, given the current model parameters, can be used. To set this
option the following configuration entries must be added:
MMIPRIOR = TRUE
MMITAUI = 50
The MMI estimates for the prior can themselves make use of I-smoothing onto a
dynamic ML prior. The smoothing constant for this is specified using
MMITAUI.
- static estimates: fixed prior parameters can be specified and used for
all iterations. A single MMF file can be specified on the command line using
the -Hprior option and the following configuration file entries added
PRIORTAU = 25
STATICPRIOR = TRUE
where PRIORTAU specifies the prior constant,
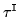 , to be
used, rather than the standard I-smoothing value.
, to be
used, rather than the standard I-smoothing value.
The best configuration option and parameter settings will be task and
criterion specific and so will need to be determined empirically. The values
shown in the tutorial section of this book can be treated as a reasonable
starting point. Note the grammar scale factors used in the tutorial are low
compared to those often used in a typical large vocabulary speech recognition
systems where values in the range 12-15 are used.
The estimation of the weights and the transition matrices have a similar
form. Only the component prior updates will be described here.
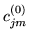 is
initialised to the current model parameter
is
initialised to the current model parameter 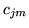 . The values are then
updated 100 times using the following iterative update rule:
. The values are then
updated 100 times using the following iterative update rule:
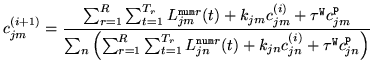 |
|
|
(8.18) |
where
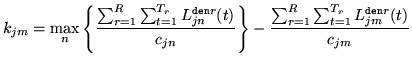 |
|
|
(8.19) |
In a similar fashion to the estimation of the means and covariance matrices
there are a range of forms that can be used to specify the prior for the
component or the transition matrix entry. The same configuration options used
for the mean and covariance matrix will determine the exact form of the prior.
For the component prior the I-smoothing weight,
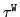 , is specified
using the configuration variable ISMOOTHTAUW. This is normally set to
1. The equivalent smoothing term for the transition matrices is set using
ISMOOTHTAUT and again a value of 1 is often used.
, is specified
using the configuration variable ISMOOTHTAUW. This is normally set to
1. The equivalent smoothing term for the transition matrices is set using
ISMOOTHTAUT and again a value of 1 is often used.
Back to HTK site
See front page for HTK Authors
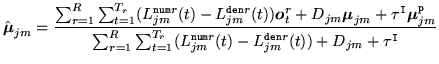
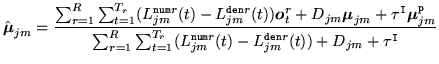
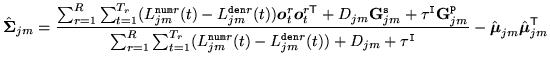
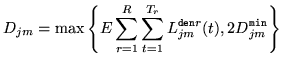
![]() is
initialised to the current model parameter
is
initialised to the current model parameter ![]() . The values are then
updated 100 times using the following iterative update rule:
. The values are then
updated 100 times using the following iterative update rule:
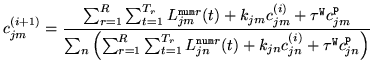
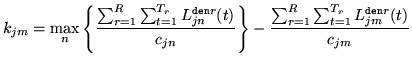
![]() , is specified
using the configuration variable ISMOOTHTAUW. This is normally set to
1. The equivalent smoothing term for the transition matrices is set using
ISMOOTHTAUT and again a value of 1 is often used.
, is specified
using the configuration variable ISMOOTHTAUW. This is normally set to
1. The equivalent smoothing term for the transition matrices is set using
ISMOOTHTAUT and again a value of 1 is often used.