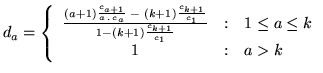In [Good 1953]14.13a method of discounting maximum likelihood estimates was proposed
whereby the count of an event occurring 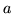 times is discounted with
times is discounted with
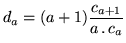 |
(14.14) |
A problem with this scheme, referred to as Good-Turing discounting,
is that due to the count in the denominator it will fail if there is a
case where 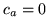 if there is any count
if there is any count 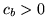 for
for
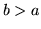 . Inevitably as
. Inevitably as 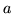 increases the count
increases the count 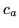 will tend towards
zero and for high
will tend towards
zero and for high 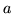 there are likely to be many such zero counts. A
solution to this problem was proposed in
[Katz 1987], which defines a cut-off value
there are likely to be many such zero counts. A
solution to this problem was proposed in
[Katz 1987], which defines a cut-off value 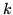 at which counts
at which counts 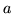 for
for 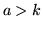 are not discounted14.14 - this is justified by
considering these more frequently observed counts as reliable and
therefore not needing to be discounted. Katz then describes a revised
discount equation which preserves the same amount of mass for the
unseen events:
are not discounted14.14 - this is justified by
considering these more frequently observed counts as reliable and
therefore not needing to be discounted. Katz then describes a revised
discount equation which preserves the same amount of mass for the
unseen events:
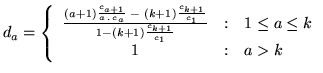 |
(14.15) |
This method is itself unstable, however - for example if
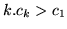 then
then 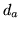 will be negative for
will be negative for
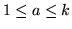 .
.
Back to HTK site
See front page for HTK Authors