The Dilating Vortex Particle
Method
The goal of the present research is the development of a vortex method for compressible flow, which takes advantage of the special properties of the incompressible method to the extent possible. The method can be applied to vortical flows for the computation of both the dynamics of the vorticity as well as the sound produced by its motion. In order to satisfy the compressible equations of motion, the particles are allowed to change volume and will carry fluid dilatation (the divergence of the velocity), entropy, enthalpy and density. Because quantities such as dilatation and enthalpy do not in general remain compact as vorticity does, but will often radiate as acoustic waves, the region of particle coverage will necessarily be larger than in the incompressible case. However, the acoustic farfield can be extrapolated from the nearfield through the use of a Kirchhoff surface, and thus coverage can still be quite limited.
A method has been developed for the solution of two-dimensional, unbounded flows. It has been succesfully applied to a variety of problems, including a co-rotating vortex pair, two pairs of leapfrogging vortices, and the passage of an expansion wave across an entropy hole. Results from these examples follow (click to see larger images):
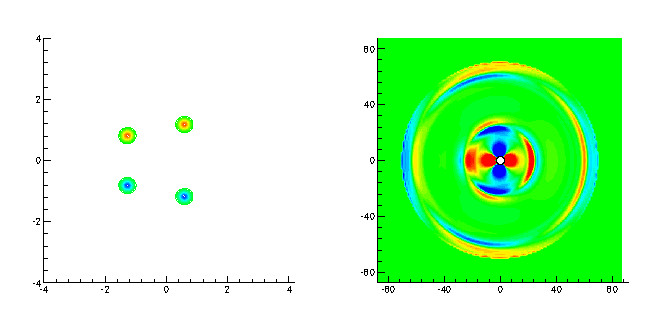 |
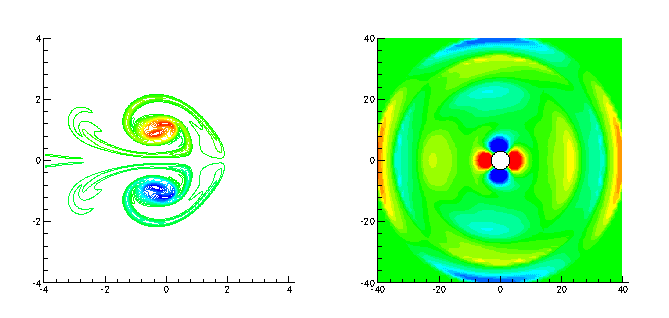 |
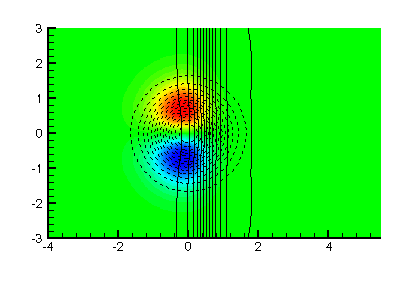 |