Effective Optical Properties of Nanoporous Materials - Simulations

Background
As previsouly mentioned, the optical properties of thin films can be tuned by introducing nanopores with different shape, size, and spatial distribution. The complex index of refraction (m=n-ik) of nanoporous thin films with various morphologies can be determined for incident electromagnetic waves by numerically solving Maxwell's equations. Here, n is the index of refraction and k is the absorption index. Polarization of an incident electromagnetic wave describes the direction of the electric field with respect to the plane of incidence defined by the Poynting vector and the normal vector of the surface on which it is incident. In transverse electric (TE) plane waves, the electric field is perpendicular to the plane of incidence while it is in that plane for transverse magnetic (TM) plane waves. Any arbitrary plane wave can be described as some combination of TE and TM waves. For a dense homogeneous film, the normal vector of the surface and the Poynting vector are collinear such that the plane of incidence and hence polarization cannot be defined. For a heterogeneous film such as the films considered here, the normal vector is no longer collinear with the Poynting vector allowing polarization to be defined that causes changes in transmittance and reflectance. The numerical results can then be compared with predictions from widely used effective medium approximations (EMAs).

Experimental data for the effective dielectric constant and index of refraction of nanoporous media reported in the literature for various materials, morphologies, porosities, and pore sizes proves inconclusive for determining the best effective medium model. Given the considerable contradictions among experimental studies, a numerical approach is considered here to assess the validity of the EMA.

Effective Medium Approximations

Various effective medium approximations (EMA) have been proposed to treat heterogeneous media as homogeneous with some effective properties.

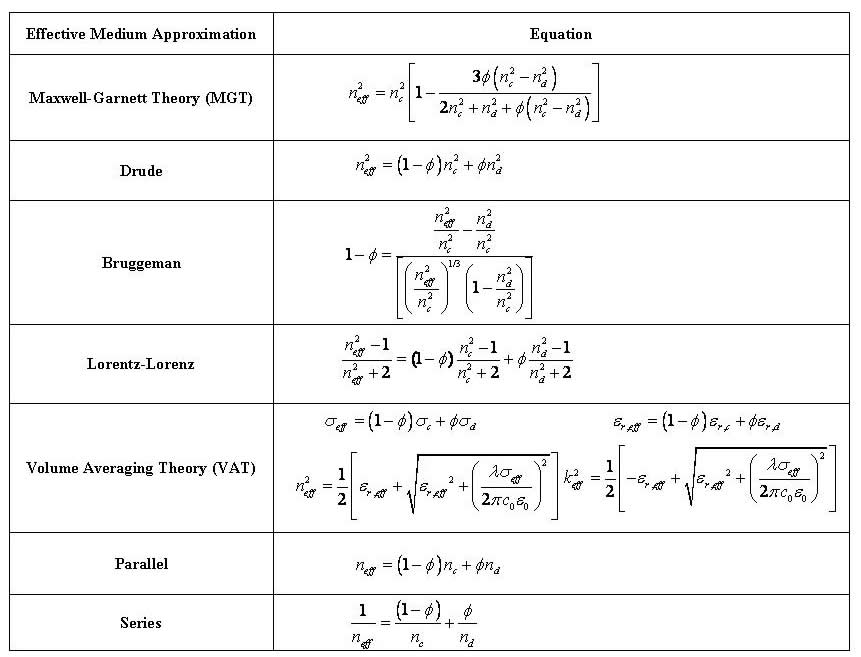
  1. Most EMAs were developed to predict the effective refraction index but not for the absorption index.
  2. No model accounts for pore size, shape, or spatial arrangements or for polarization of the incident wave.
  3. The Maxwell-Garnett model was developed for the effective dielectric constant (not for the refractive index) of monodispersed spherical metallic nanoparticles arranged as a simple cubic lattice in a dielectric medium (0 £f £ 52%).
  4. The Bruggeman model extends Maxwell-Garnett model to polydisperse particles.
  5. The volume averaging theory model indicates that the effective refractive index neff depends not only on nc and nd but also on kc and kd. Similarly for the effective absorption index keff.
  6. It is unclear to the user what model to use for any arbitrary mesoporous or nanocomposite materials.
Approach

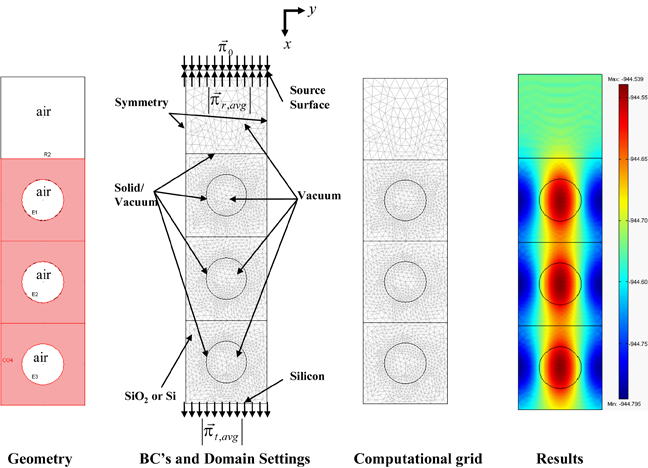
The figure below illustrates the physical model of the nanocomposite thin films studied, along with the associated coordinate system, boundary conditions, and finite element grid. The model corresponds to a nanoporous thin film with three cylindrical pores. Note that this figure is illustrative only with three pores. However, actual numerical computations are performed for a much larger number of pores (L/D≥150), different porosities, and varying pore spatial arrangement. Both continuous (mc=nc−ikc) and dispersed (md=nd−ikd) phases are assumed to be homogenous and isotropic and to have the same optical properties as the bulk material. The thin film is deposited onto a non-absorbing dense substrate (medium 3, n3, k3=0) and surrounded by vacuum (medium 1, n1=1.0, k1=0). The nanocomposite thin film is treated as homogeneous (medium 2) with some effective optical properties neff and keff. A linearly polarized plane wave is incident normal to the top surface of the absorbing thin film and travels in the x-direction through the two-dimensional thin film. FEMLAB 3.1 is used to numerically solve Maxwell's equations in two-dimensions in the frequency domain applying the Galerkin finite element method on unstructured meshes. The effective complex index of refraction is retrieved through an inverse method by minimizing the root mean square of the relative error for transmittance and reflectance between numerical data and theoretical predictions from thin film optics.

Results

Effect of Film Thickness

In order to explore the effect of film thickness on the optical properties of nanoporous thin films, the retrieved index of refraction is calculated as a function of the ratio of the film thickness L to the diameter of the spherical pores D for a film with 19.63% porosity and three different pore diameters equal to 1, 10, and 100 nm. For each data set, only the film thickness L is varied. Then, several conclusions can be drawn:

  1. For any given pore diameter D and small values of film thickness L, the effective index of refraction is a function of L and D. Therefore the effective medium approach is not valid.
  2. For incident TE waves, beyond a critical thickness Lcr, the effective medium approach is valid and an effective index of refraction can be defined as a function of porosity and of the constituent phase indices of refraction nc and nd only. However, for incident TM waves, this conclusion does not hold since the optical properties are a function of pore spatial arrangement (see "Effect of Pore Spatial Arrangement" below).
  3. The magnitude of the critical film thickness Lcr is a function of the pore diameter and the incident radiation wavelength k. The Lcr/D values are arbitrarily defined so that all subsequent values of neff fall within 0.05% of the converged solution. In the present case, Lcr is found to be up to 50 times the pore diameter for 100 nm pores.

Note that similar results are obtained for the absorption index k.

Effect of Pore Size and Pore Shape

For films thicker than the critical thickness Lcr, the effective index of refraction and absorption index are indepenedent of the pore diameter and shape.

Effective Medium Models for TE Waves

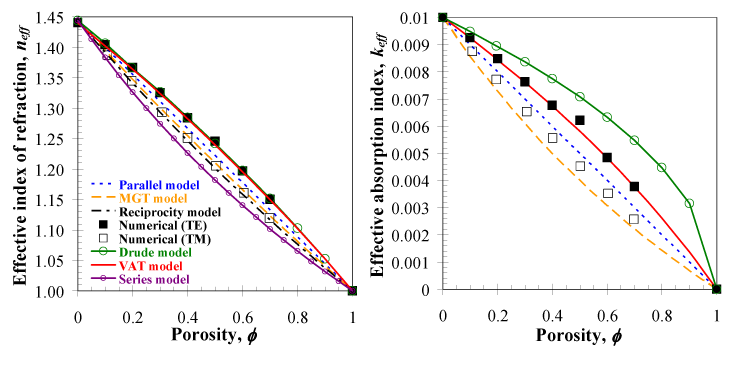
To determine which effective medium model accurately predicts the optical properties for TE waves, an nanoporous thin film with nc=1.44, kc=0.01, nd=1.0, and kd=0 over the spectral range from 400 to 900 nm is considered. The figure below compares the effective index of refraction neff and absorption index keff for both TE and TM waves with various effective medium models as a function of porosity. The series and reciprocity models are excluded for the effective absorption index keff since kd=0. As expected, neff and keff decrease with increasing porosity. The results show that the VAT model agrees well with the numerical results for TE waves.

Effective Medium Models for TM Waves

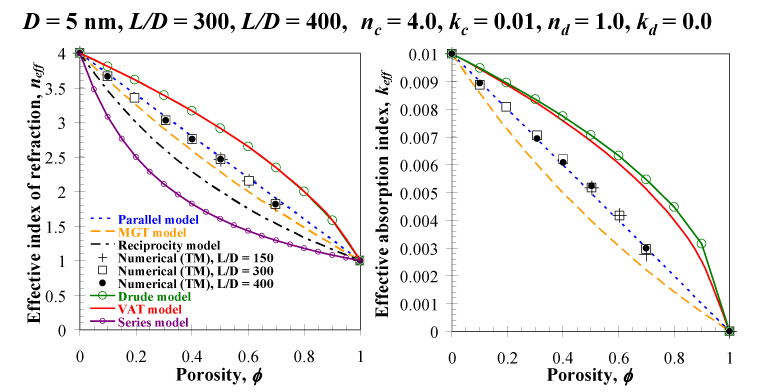
To determine which effective medium model accurately predicts the optical properties for TM waves, an imaginary nanoporous thin film with equally spaced pores and with nc=4.0, kc=0.01, nd=1.0, and kd=0 over the visible spectrum from 400 to 900 nm is considered. With a continuous phase index of refraction nc=4.0, the relative difference between the various effective medium models for neff and keff can reach up to 46.0% and 72.7%, respectively. This large difference allows for closer examination and validation of the effective medium models for TM waves. The figure below establishes that the numerical predictions for neff and keff agree well with the parallel model. Indeed, the maximum relative error between the numerical results and the predictions from the parallel model for neff and keff was 4.3% and 1.6%, respectively. The VAT and the Drude model overpredict the numerical results while the MGT, reciprocity, and series models underpredict them.

Effect of Pore Spatial Arrangement

In order to study the effect of pore spatial arrangement on effective optical properties, thin films with anisotropic morphology were examined by varying the distance between pores in the x-and y-directions. The figure below illustrates the physical model of absorbing nanocomposite thin films with anisotropic morphology and various aspect ratios a/b where a and b refer to the vertical and horizontal distance between pores, respectively. Note that a/b=1 corresponds to a thin film of isotropic morphology where the distance between pores is the same in all directions.

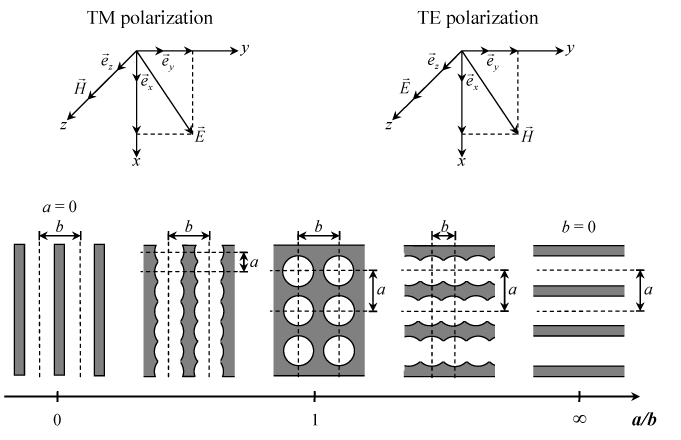
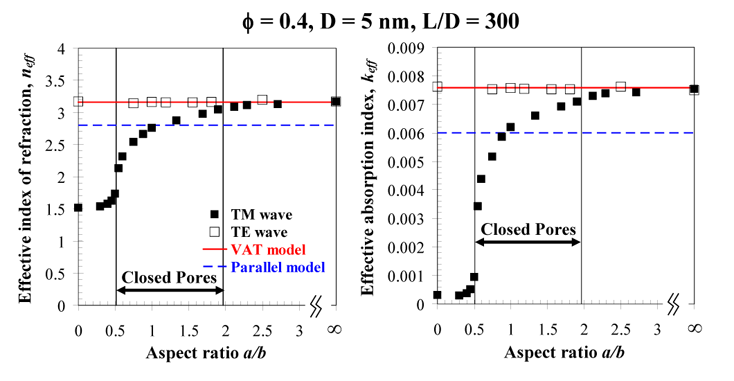
The figure below shows the effective index of refraction neff and the effective absorption index keff as functions of aspect ratio a/b for both TE and TM waves incident on nanoporous thin films with constant porosity of 0.4. The solid vertical lines at a/b=0.51 and a/b=1.96 correspond to lower and upper bounds of thin films with closed pores. For a/b outside this interval, pores intersect with one another and are no longer closed. In brief, for TE polarization, the effective optical properties are independent of the pore spatial arrangement. They depend only on porosity and are in good agreement with the VAT model. This can be attributed to the fact that the normal vector of all cylindrical pores simulated is confined to the x–y plane and is always perpendicular to the electric field of a TE polarized plane wave. Thus, polarization has no effect on reflection and refraction across the interface. In contrast, for TM waves, the effective index of refraction neff and the effective absorption index keff increase with increasing a/b. As a/b goes to infinity, neff and keff converge to the numerical values found for TE polarization which matches the VAT model predictions. Indeed, as a/b tends to infinity, the morphology of the thin film approaches that of a superlattice consisting of alternating thin films of continuous and dispersed phases for which the normal vectors of all interfaces are collinear with the Poynting vector. Then, the plane of incidence and thus, the polarization cannot be defined. However, for a/b ratios other than infinity, the normal vector of the continuous-dispersed interfaces is not collinear to the Poynting vector at all points around the cylindrical pores.

Publications

M. M. Braun and L. Pilon, 2006. Effective Optical Properties of Non-Absorbing Nanoporous Media. Thin Solid Films, Vol. 496, No.2, pp.505-514. doi:10.1016/j.tsf.2005.08.173.

A. Garahan, L. Pilon, J. Yin, and I. Saxena, 2007. Effective Optical Properties of Absorbing Nanoporous and Nanocomposite Thin-Films. Journal of Applied Physics, Vol. 101, No.11, 014320. doi:10.1063/1.2402327.

A. Navid and L. Pilon, 2008. Effect of Polarization and Morphology on the Optical Properties of Absorbing Nanoporous Thin Films, Thin Solid Films, Vol. 516, pp.4159-4167. doi:10.1016/j.tsf.2007.10.117

N. Hutchinson , T. Coquil, E. Richman, S. Tolbert, and L. Pilon, 2010. Reflectance of Surfactant-Templated Mesoporous Silica Thin Films : Simulations Versus Experiments. Thin Solid Films, Vol. 518, pp. 2134-2140. doi: 10.1016/j.tsf.2009.08.006

N. Hutchinson , A. Navid, T. Coquil, and L. Pilon, 2010. Effective Optical Properties of Highly Ordered Mesoporous Thin Films. Thin Solid Films, Vol. 518, pp. 2141-2146. doi: 10.1016/j.tsf.2009.08.048