Abstract
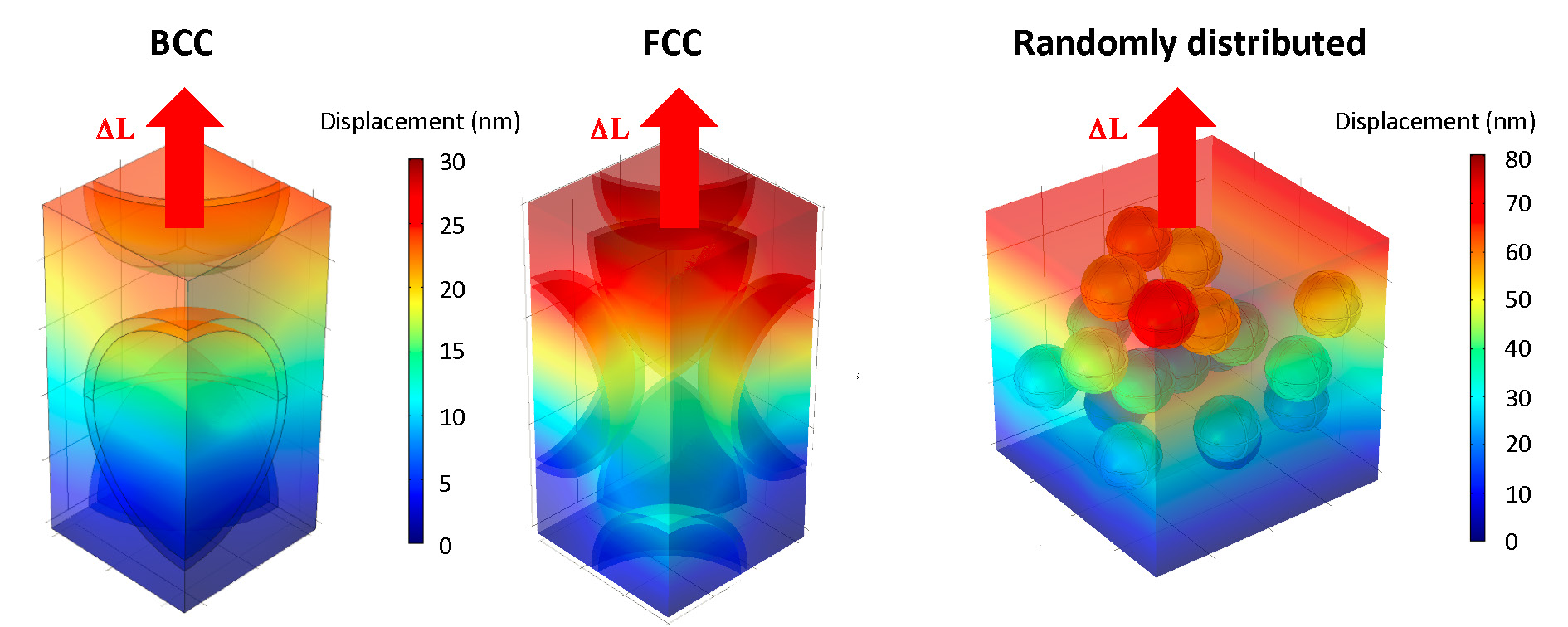
The effective Young’s modulus and Poisson’s ratio of spherical monodisperse and polydisperse core-shell particles ordered or randomly distributed in a continuous matrix were predicted using detailed three-dimensional numerical simulations of elastic deformation. The effective elastic moduli of body-centered cubic (BCC) and face-centered cubic (FCC) packing arrangements of monodisperse microcapsules and those of randomly distributed monodisperse or polydisperse microcapsules were identical. The numerical results were also compared with predictions of various effective medium approximations (EMAs) proposed in the literature. The upper bound of the EMA developed by Qiu and Weng (1991) was in good agreement with the numerically predicted effective Young's modulus for BCC and FCC packings and for randomly distributed microcapsules. The EMA developed by Hobbs (1971) could also be used to estimate the effective Young's modulus when the shell Young's modulus was similar to that of the matrix. The EMA developed by Garboczi and Berryman (2001) could predict the effective Poisson’s ratio, as well as the effective Young's modulus when the Young's modulus of the core was smaller than that of the matrix. These results can find applications in the design of self-healing polymers, composite concrete, and building materials with microencapsulated phase change materials, for example.
Schematics and Assumptions
The deformation of composite materials consisting of a (i) matrix containing monodisperse spherical microcapsules with simple cubic (SC), body-centered cubic (BCC), or face-centered cubic (FCC) packing arrangements and of (ii) monodisperse and polydisperse microcapsules randomly distributed throughout the matrix was simulated numerically. Figure 1 shows a quarter of a simulated unit cell with (a) SC, (b) BCC, and (c) FCC packing arrangements along with the associated Cartesian coordinate system. Figure 2 shows examples of simulated (a) monodisperse and (b) polydisperse microcapsules randomly distributed in a continuous matrix.
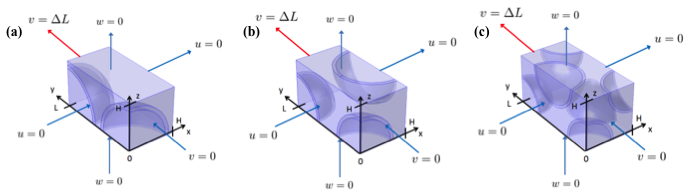
Figure 1. Schematics of core-shell particles with an (a) SC, (b) BCC, and (c) FCC packing arrangement, and the associated Cartesian coordinate system. Five of six faces are fixed, and a uniform normal displacement is applied to the final face.
Assumptions:
|
|
Results and Discussion
Table 1 reports numerical predictions of the effective Young’s modulus Eeff and the effective Poisson’s ratio νeff of three-component composite structures consisting of various core and shell volume fractions of monodisperse and polydisperse microcapsules randomly distributed in a continuous matrix with a unit cell length L = 75 μm. It also shows the values of Eeff and νeff for equivalent composites consisting of monodisperse microcapsules with BCC and FCC packing arrangements having nearly identical core and shell volume fractions φc and φs. In the baseline case, the core, shell, and matrix Young’s moduli were taken as Ec = 55.7 MPa, Es = 6.3 GPa, and Em = 16.75 GPa, while their Poisson’s ratios were νc = 0.499, νs = 0.34, and νm = 0.2, respectively. These properties corresponded to a three-component PCM composite consisting of microencapsulated paraffin wax with a polymeric shell embedded in a cement matrix. Table 1 establishes that Eeff and νeff were independent of spatial and size distributions. In other words, BCC and FCC packing arrangements were representative of the elastic behavior of monodisperse or polydisperse microcapsules randomly distributed in a matrix.
Table 1. Effective Young’s modulus Eeff and effective Poisson’s ratio νeff of three-phase composites consisting of p microcapsules either monodisperse or polydisperse and either in ordered packing arrangements or randomly distributed in a continuous matrix with until cell length L. Here, Ec = 55.7 MPa, Es = 6.3 GPa, Em = 16.75 GPa, νc = 0.499, νs = 0.34, and νm = 0.2.
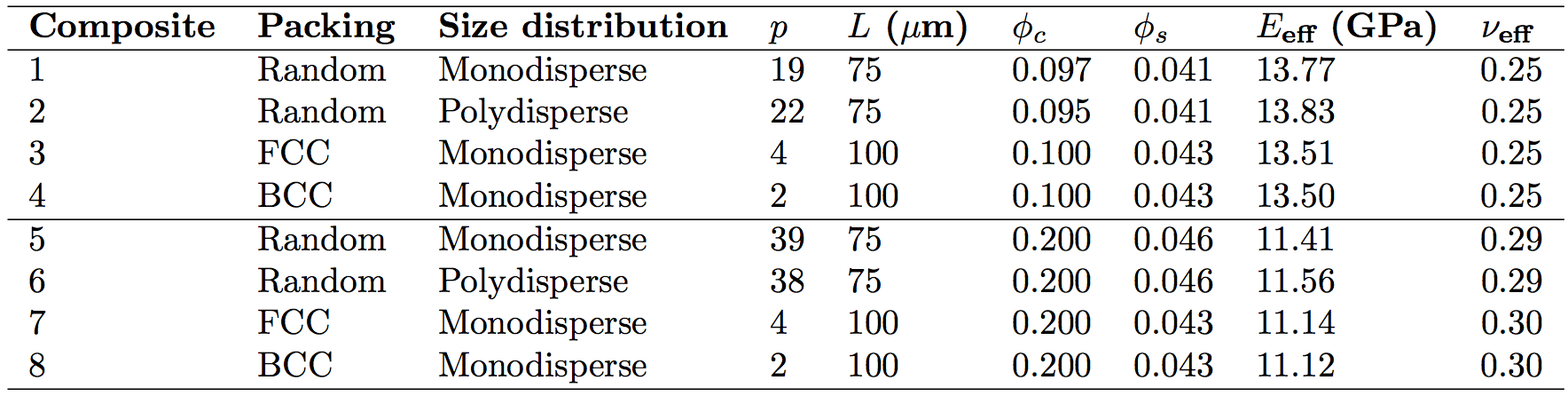
Figure 3 plots (a) the effective Young’s modulus Eeff and (b) the effective Poisson’s ratio νeff of a three-component core-shell-matrix composite as functions of core volume fraction φc ranging from 0 to 0.3 for a constant shell volume fraction φs of 0.043. The microcapsules either monodispere or polydisperse and either packed in SC, BCC, or FCC arrangements or randomly distributed in the matrix. Figure 3 illustrates that the predictions of the effective Young’s modulus and Poisson’s ratio were identical for monodisperse spheres in BCC or FCC packing structrues and for randomly distributed mono- and poly-dispersed microcapsules, as previously observed in Table 1. Predictions for SC packing differed from other spatial distributions. Figure 3 also plots the effective Young’s modulus and Poisson’s ratio as a function of core volume fraction predicted by several EMAs found in the literature. Among the three-component EMAs, the D-EMT model [1], the Qiu and Weng [2] upper bound, and the model by Dunn and Ledbetter [3] gave the best agreement with numerical predictions of Eeff and νeff for BCC and FCC packing arrangements and randomly distributed monodisperse and polydisperse microcapsules. In addition, predictions of the effective Young’s modulus by the EMA developed by Hobbs [4] for two-component systems fell with 2% of those obtained numerically for BCC and FCC packing arrangements for the cases considered by ignoring the presence of the shell. This led to acceptable results because the shell volume fraction was small and Es was similar to Em.
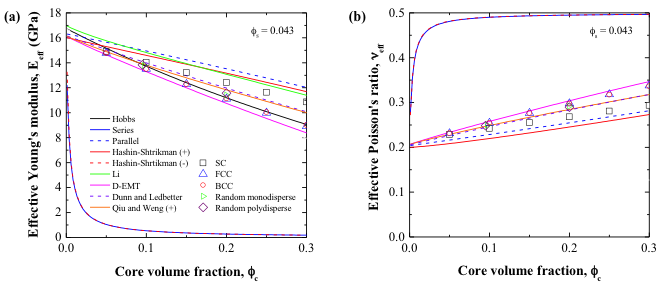
Figure 3. (a) Effective Young’s modulus Eeff and (b) effective Poisson’s ratio νeff of a core-shell-matrix composite as functions of the core volume fraction φc for constant shell volume fraction φs = 0.043. Here, Ec, Es, Em, νc, νs, and νm were those of the baseline case.
Figures 4a-4d plot the ratio Eeff/Em of monodisperse core-shell particles packed in SC, BCC, or FCC structures as a function of the ratio Ec/Em ranging from 10-4 to 104 for ratios Es/Em equal to 0.1, 1, 10, and 100, respectively. The ratio Eeff/Em is shown for two values of matrix Young’s moduli Em, namely 1 and 10 GPa. Then, the shell Young’s modulus Es was adjusted to achieve the desired Es/Em ratio. In all cases, the core and shell volume fractions were 0.3 and 0.1, respectively, and the Poisson’s ratios of the core, shell, and matrix were those of the baseline case. Figure 4 indicates that the ratio Eeff/Em was dependent only on the ratios Ec/Em and Es/Em, rather than on the Young’s moduli of each constituent component. It is interesting to note that the ratio Eeff/Em showed little dependence on Ec/Em in the limiting cases when Ec/Em was very small (soft core) or very large (hard core). This suggests that for microencapsulated PCM-concrete composites with a soft care, a variance in the Young’s modulus of the PCM has little effect on Eeff. Additionally, Figure 4 plots the EMAs for Eeff that gave the best agreement with numerical results. The predictions by the upper bound of the Qiu and Weng model agreed the most closely with numerical predictions of Eeff for microcapsules with BCC or FCC packings across the ranges of Ec/Em considered. For cases when Ec was smaller than Em, such as for microencapsulated PCM in concrete, predictions from the D-EMT EMA were in better agreement with numerical predictions than those by the Qiu and Weng model. Finally, for the case when Es/Em = 1, the predictions of the EMA proposed by Hobbs fell within 3% of those for BCC and FCC packing arrangements.
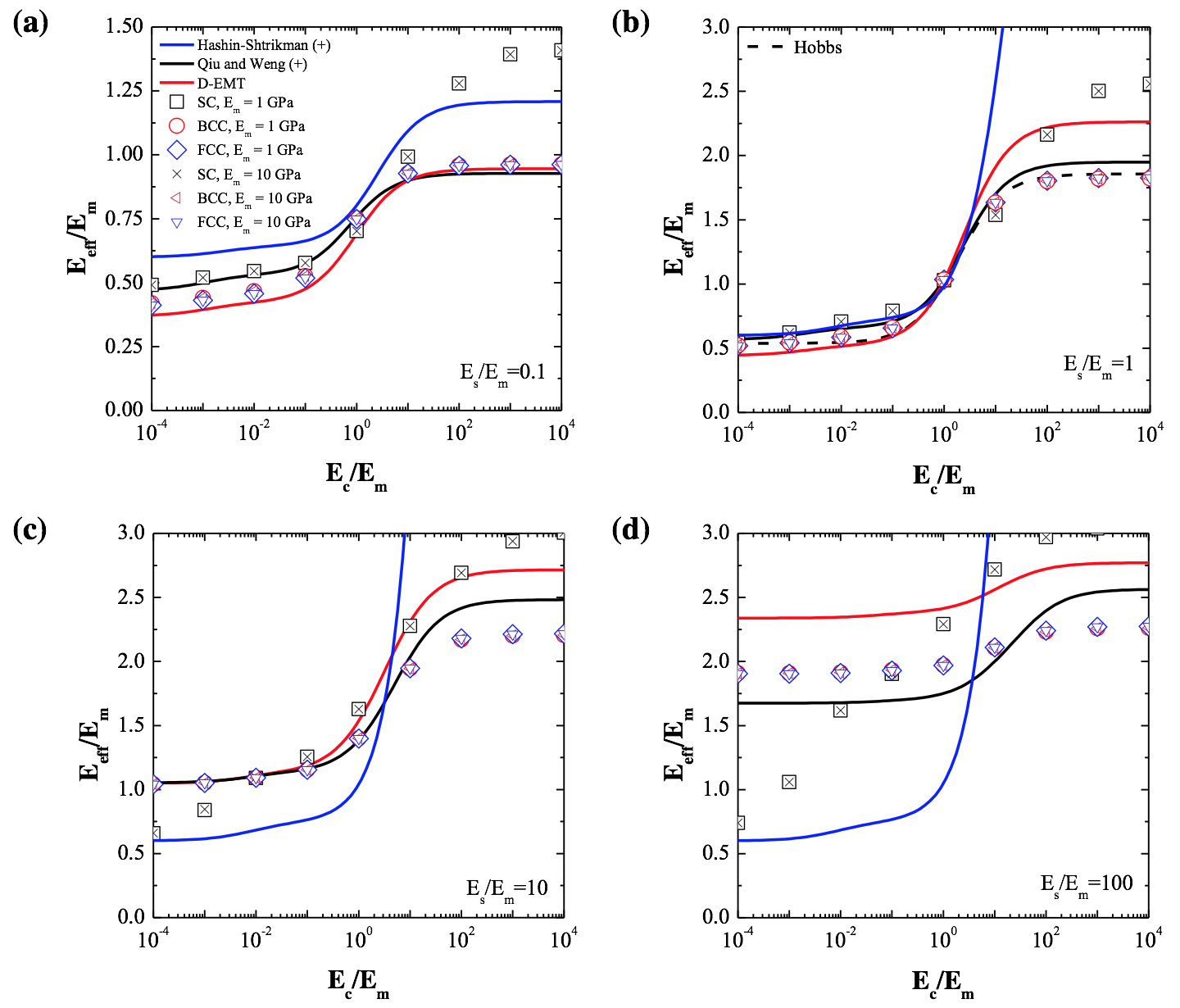
Figure 4. Ratio Eeff/Em of a core-shell-matrix composite for SC, BCC, or FCC packings as a function of the ratio Ec/Em equal to (a) 0.1, (b) 1, (c) 10, and (d) 100. Predictions of EMAs are also shown including the D-EMT EMA [1], the upper Qiu and Weng bound [2], and the Hobbs model [4] (for Es = Em). Here, φc = 0.3, φs = 0.1, νc = 0.499, νs = 0.34, and νm = 0.2.
Conclusion
- Detailed 3D simulations were performed for elastic deformations in three-component composites consisting of monodisperse or polydisperse microcapsules ordered in SC, BCC, or FCC packing or randomly distributed in a continuous matrix.
- The effective Young’s modulus Eeff and effective Poisson’s ratio νeff were identical for BCC, FCC, and randomly distributed microcapsule packing arrangements over a wide range of core and shell volume fractions and constituent mechanical properties.
- The ratio Eeff /Em was found to be a function of the core and shell volume fractions φc and φs and of the ratios Ec/Em and Es/Em. However, it was generally independent of νm and of the Poisson’s ratios νc/νm and νs/νm.
- The effective Poisson’s ratio νeff was found to be a function of φc and φs, the ratios Ec/Em and Es/Em, and the shell and matrix Poisson’s ratios νs and νm.
- Accurate effective medium approximations (EMAs) for composites’ effective moduli were identified:
- The upper bound of the EMA by Qiu and Weng [2] predicted accurately the numerical results of Eeff for BCC and FCC packings and randomly distributed microcapsules.
- The D-EMT EMA developed by Garboczi and Berryman [1] gave excellent predictions of Eeff for cases when Ec/Em was less than 1.
- The EMA developed by Hobbs [4] for two- component composites gave accurate predictions of Eeff when the shell Young’s modulus Es was similar to that of the matrix Em.
- The D-EMT EMA gave the best agreement with numerical predictions of the effective Poisson’s ratio for BCC and FCC packing arrangements in the range of parameters considered.
These results can be used to inform the selection of materials for PCM composites for building applications and for other three-phase core-shell- matrix composites such as self-healing polymer composites. In the meantime, efforts are underway to confront these numerical results with experimental measurements for concrete containing microencapsulated PCMs.
References
[1] E.J. Garboczi and J.G. Berryman, "Elastic moduli of a material containing composite inclusions: effective medium theory and finite element computations", Mechanics of Materials, vol. 33 (8) 455-470, 2001.
[2] Y. P. Qiu and G. J. Weng, "Elastic moduli of thickly coated particle and fiber-reinforced composites", Journal of Applied Mechanics, 58, 388-398, 1991.
[3] M. L. Dunn and H. Ledbetter, "Elastic moduli of composites reinforced by multiphase particles", Journal of Applied Mechanics, 62, 1023-1028, 1995.
[4] D. W. Hobbs, "The dependence of the bulk modulus, Young’s modulus, creep, shrinkage and thermal expansion of concrete upon aggregate volume concentration", Materiaux et Construction, 4 (2) 107-114, 1971.
Publication
B. Young, A. Fujii, A. Thiele, A. Kumar, G. Sant, E. Taciroğlu, and L. Pilon, 2016. Effective Elastic Moduli of Core-Shell-Matrix Composites, Mechanics of Materials, Vol. 92, pp. 94-106. doi: 10.1016/j.mechmat.2015.09.006 pdf
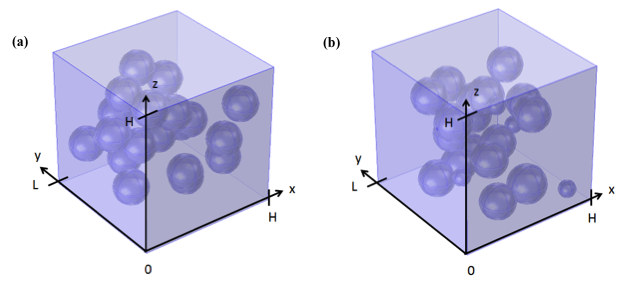 Figure 2. Schematics of unit cells used for numerical simulations with (a) monodisperse microcapsules, φc = 0.097, and φs = 0.041 as well as with (b) polydisperse microcapsules, φc = 0.095, and φs =0.041.
Figure 2. Schematics of unit cells used for numerical simulations with (a) monodisperse microcapsules, φc = 0.097, and φs = 0.041 as well as with (b) polydisperse microcapsules, φc = 0.095, and φs =0.041.