Abstract
This study presents detailed numerical simulations predicting the effective thermal conductivity of spherical monodisperse and polydisperse core-shell particles ordered or randomly distributed in a continuous matrix. First, the effective thermal conductivity of this three-component composite material was found to be independent of the capsule spatial distribution and size distribution. In fact, the study established that the effective thermal conductivity depended only on the core and shell volume fractions and on the core, shell, and matrix thermal conductivities. Second, the effective medium approximation reported by Felske [1] was in very good agreement with numerical predictions for any arbitrary combination of the above-mentioned parameters. These results can be used to design energy efficient composites, such as microencapsulated phase change materials in concrete and/or insulation materials for energy efficient buildings.
Felske Model
Felske [1] derived a model, using the self-consistent field approximation, to predict the effective thermal conductivity of monodisperse spherical capsules randomly distributed in a continuous matrix. In the absence of contact resistance at the shell-matrix interfaces, the model can be expressed as,
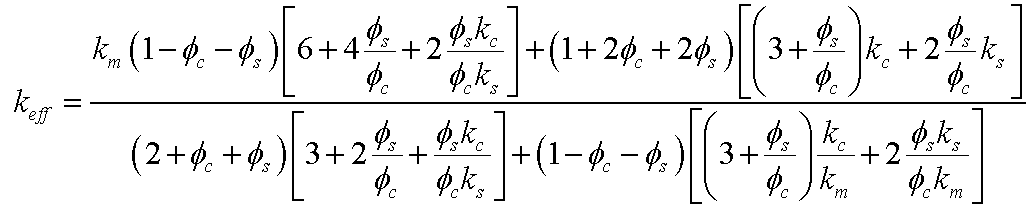
where kc, ks, and km are the thermal conductivities of the core, shell, and matrix materials, respectively. Similarly, ϕc, ϕs, and ϕm are the volume fractions of the core, shell, and matrix materials, respectively.
Schematics and Assumptions
The present study examined various composite representative volumes consisting of different packing arrangements of monodisperse and polydisperse spherical capsules distributed in a continuous matrix.
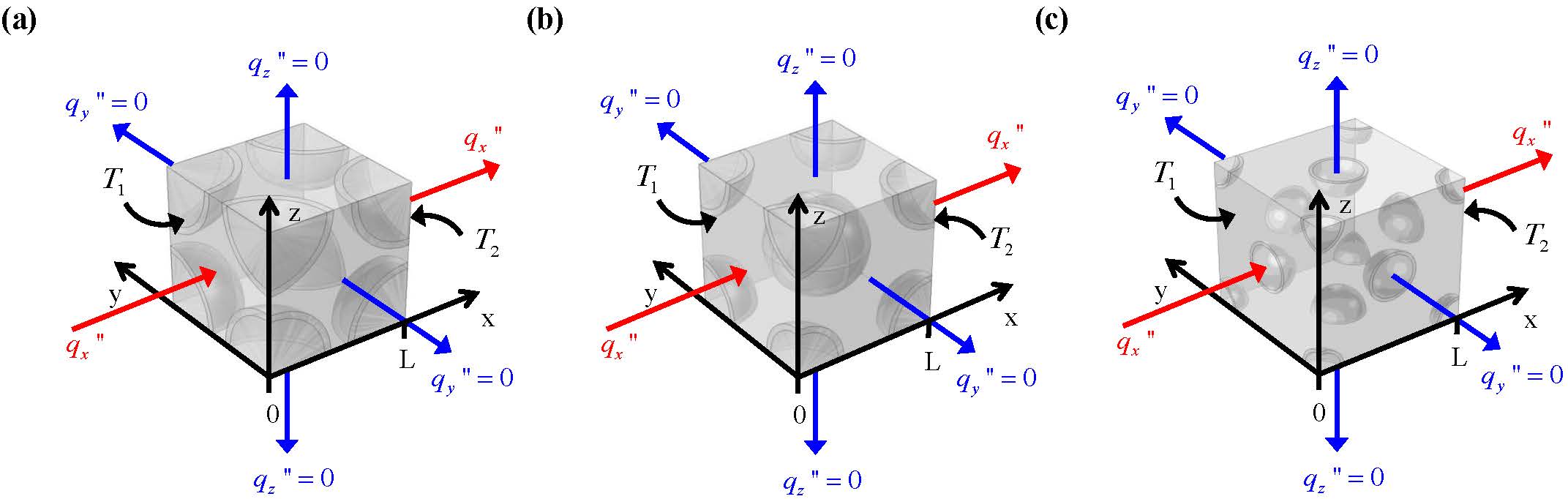
Figure 1. Schematic and computational domain of a single unit cell consisting of capsules distributed in a continuous matrix with (a) simple, (b) body-centered, and (c) face-centered cubic packing arrangement. Core and shell diameters and unit cell length corresponding to core and shell volume fractions ϕc and ϕs were denoted by Dc, Ds, and L, respectively.
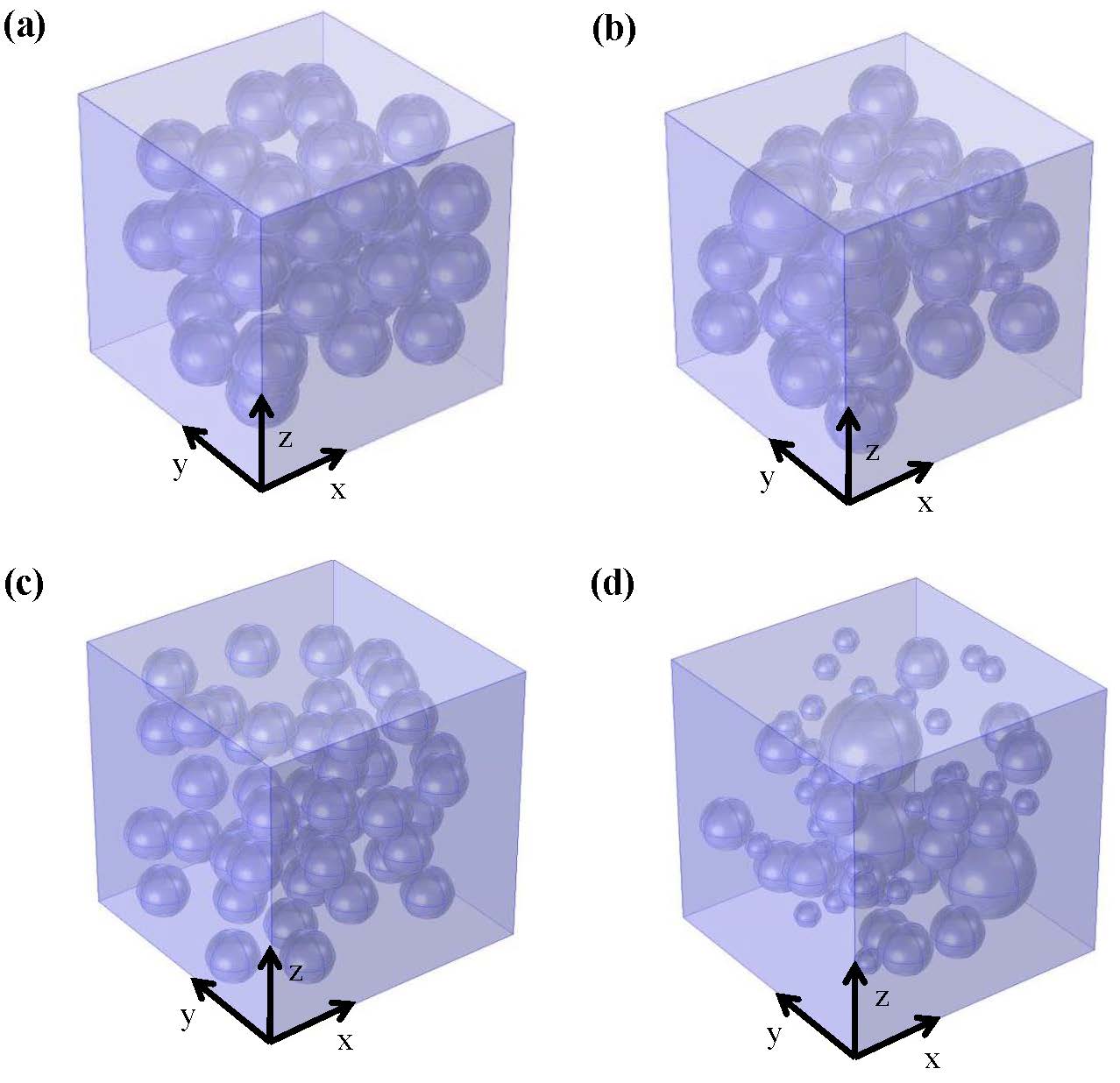
Figure 2 shows examples of computational volumes consisting of 38 to 61 monodisperse or polydisperse capsules randomly distributed in a continuous matrix. To make the problem mathematically tractable, the following assumptions were made:
|
Figure 2. Computational cells containing monodisperse capsules with (a) p = 39, L = 75 μm, ϕc = 0.198, and ϕs = 0.041, and (c) p = 49, L = 100 μm, ϕc = 0.105, and ϕs = 0.045, as well as polydisperse capsules with (b) p = 38, L = 75 μm, ϕc = 0.197, and ϕs = 0.075, and (d) p = 61, L = 100 μm, ϕc = 0.095, and ϕs = 0.035. |
Governing equations and boundary conditions
Under the above assumptions, the local temperatures in the core, shell, and matrix denoted by Tc, Ts, and Tm were governed by the steady-state heat diffusion equation in each domain, given by,
![]() .
.
These equations were coupled through the boundary conditions. Heat conduction took place mainly in the x-direction of the unit cell or representative cube [Figures 1 or 2] by imposing the temperature on the faces of the cube located at x = 0 and x = L such that for 0 ≤ y ≤ L and 0 ≤ z ≤ L,
![]()
By virtue of symmetry, the heat flux through the four lateral faces vanished, i.e.,
![]()
where q"y(x,y,z) and q"z(x,y,z) are the heat fluxes along the y- and z-axes, respectively. They are given by Fourier's law, i.e., q"y= -k∂T/∂y and q"z= -k∂T/∂z. The boundary temperatures on the faces x = 0 and x = L were taken as To = 294 K and TL = 292 K. Coupling between the temperatures of the different domains was achieved by imposing continuous heat flux across their interfaces, i.e.,
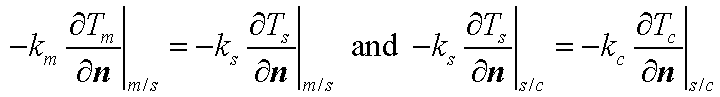
where n is the unit normal vector at any given point on the matrix/shell and shell/core interfaces, designated by subscript m/s and s/c, respectively.
Results and Discussion
Table 1 compares the numerically predicted effective thermal conductivity keff of ten composite microstructures to that predicted by the Felske model. Cases 1 and 2 indicate that the numerically predicted keff was the same for composites with monodisperse or polydisperse capsules for the same values of ϕc, &ϕs, kc, ks, and km. Table 1 also shows that keff predicted by the Felske model fell within 0.25% of numerical predictions for a wide range of constituent thermal conductivities kc, ks, and km and volume fractions ϕc and ϕs.
Table 1. Numerical and analytical predictions of the effective thermal conductivity of composites consisting of monodisperse or polydisperse capsules randomly distributed in a continuous matrix. The average outer diameter and thickness of the shell are Ds,avg = 18 μm and ts = 1 μm.
Figure 3 shows the effective thermal conductivity keff of a composite containing monodisperse capsules as a function of (a) the core volume fraction ϕc and (b) the shell volume fraction ϕs. The desired volume fractions were imposed by either adjusting the relevant diameter (Dc or Ds) while holding the unit cell length L constant or by adjusting the unit cell length L and holding the relevant diameter constant. Figures 3a and 3b establish that keff depended only on ϕc and ϕs and not on the individual geometric parameters Dc, Ds, and L.
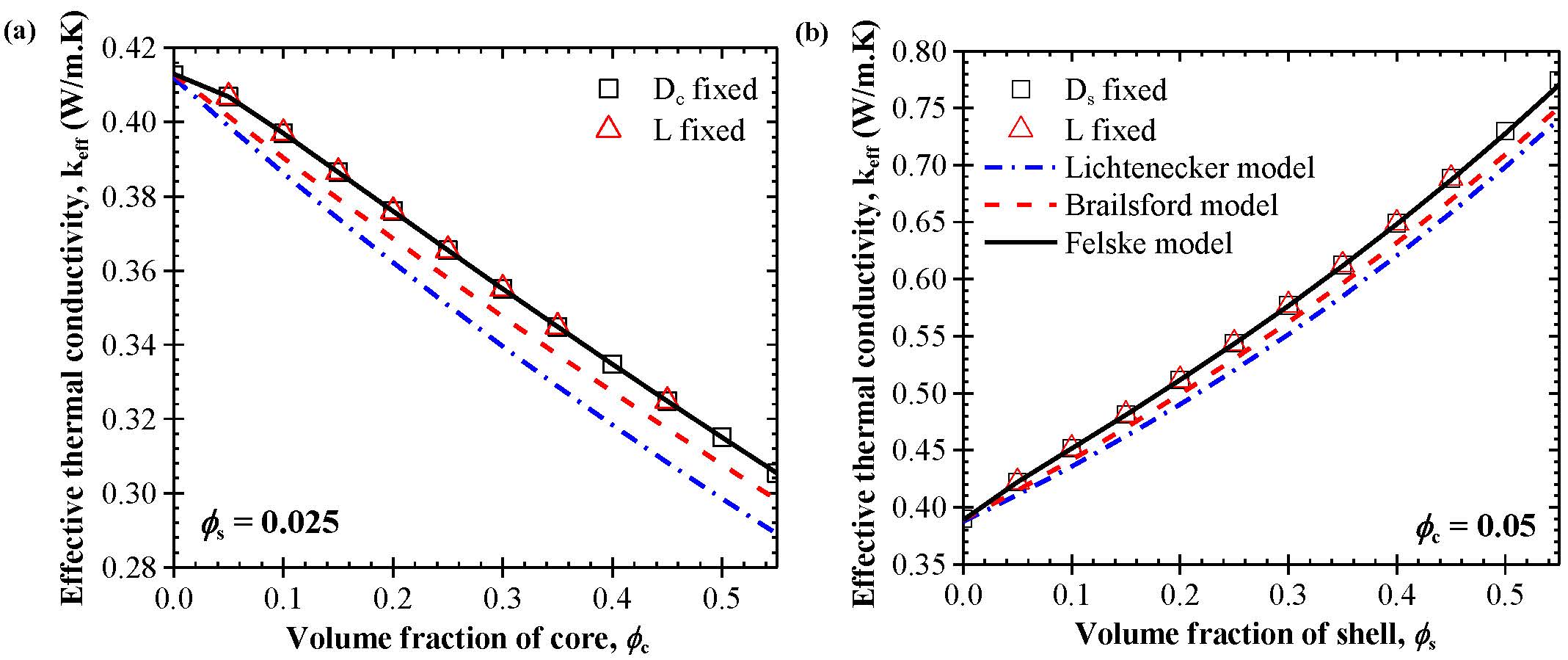
Figure 3. Effective thermal conductivity for (a) different values of ϕc with ϕs = 0.025 and (b) different values of ϕs with Φc = 0.05. The volume fractions were varied by adjusting either the diameter or unit cell length. Here, kc = 0.21 W/mK, ks = 1.3 W/mK, and km = 0.4 W/mK. Predictions by the Lichtenecker, Brailsford, and Felske models are also shown.
Figure 4 plots the effective thermal conductivity keff of a composite material containing monodisperse capsules as a function of the thermal conductivity of the matrix km, core kc, and shell ks, respectively. Figure 4 shows that the Felske model predicted the effective thermal conductivity keff of composites containing monodisperse capsules within the estimated numerical uncertainty for all volume fractions considered and for a wide range of constituent material thermal conductivities.
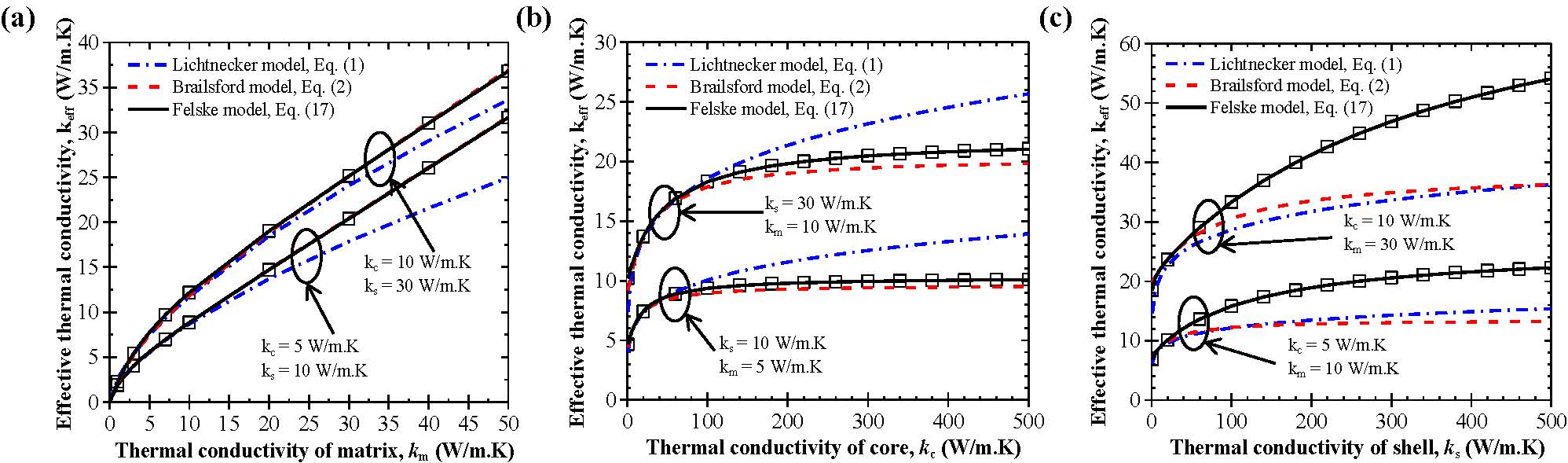
Figure 4. Effective thermal conductivity keff of core-shell composite as a function of the thermal conductivity of the (a) continuous km, (b) core kc, and (c) shell ks phase obtained numerically and predicted by the Lichtenecker, Brailsford, and Felske models. The volume fractions of core and shell were ϕc = 0.2 and Φs = 0.145.
Conclusion
This study established that the effective thermal conductivity was independent of the capsules' spatial distribution and size distribution. The effective thermal conductivity was found to depend solely on the core and shell volume fractions and on the core, shell, and matrix thermal conductivities. The Felske model predicted the effective thermal conductivity of the composite material within numerical uncertainty for the wide range of parameters considered. This model was used to identify conditions under which the effective thermal conductivity keff of the composite materials remained smaller than that of the matrix material. This thermal design rule will be useful in developing PCM-composite materials for energy efficient buildings.
References
- J.D. Felske, 2004. Effective thermal conductivity of composite spheres in a continuous medium with contact resistance. International Journal of Heat and Mass Transfer, Vol. 47, pp. 3453-3461. doi:10.1016/j.ijheatmasstransfer.2004.01.013
- A.M. Thiele, A. Kumar, G. Sant, and L. Pilon, 2014. Effective Thermal Conductivity of Three-Phase Composites Containing Spherical Capsules. International Journal of Heat and Mass Transfer, Vol. 73, pp. 177–185. doi: 10.1016/j.ijheatmasstransfer.2014.02.002