First Principles Thermal Modeling of Electric Double Layer Capacitors

Abstract

This study aims to develop physical modeling and understanding of the coupled electrodiffusion, heat generation, and thermal transport occurring in electric double layer capacitors (EDLCs) during constant-current cycling. To do so, the governing energy equation was derived from first principles and coupled with the modified Poisson-Nernst-Planck model for transient electrodiffusion in a binary and symmetric electrolyte. In particular, irreversible Joule heating and reversible heat generation rates due to ion diffusion, steric effects, and changes in entropy of mixing in EDLCs were rigorously formulated. Detailed numerical simulations of the temperature rise in the electrolyte were performed for planar electrodes. The results qualitatively reproduced experimental data reported in the literature under various charging/discharging conditions.

Analysis

Schematic and Assumptions

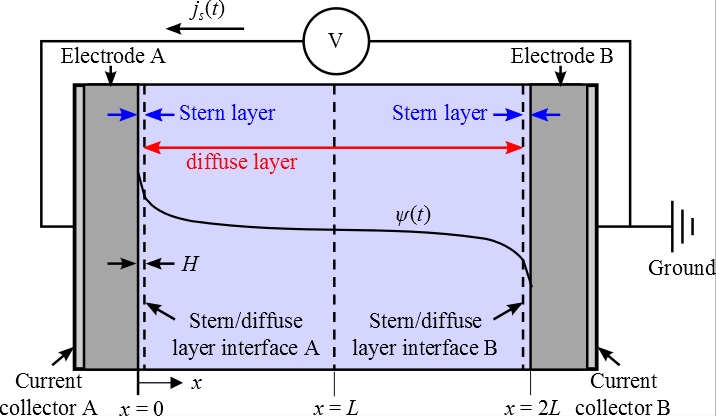Assumptions:
1. Chemical reactions and ion insertion into the electrode were absent.
2. The electrolyte was binary and symmetric.
3. Dissociation of the electrolyte was complete.
4. Bulk motion of the electrolyte was negligible.
5. The simulated EDLC was thermally insulated.
6. The Stern layer thickness H was equal to half of the effective ion diameter, i.e., H=a/2.
7. All electrolyte properties were constant and independent of temperature, except for the concentration-dependent electrolyte conductivity.

Governing Equations

For binary and symmetric electrolytes, i.e., those with symmetric valency z1=-z2=z, ion diameter a1=a2=a, and ion diffusion coefficient D1=D2=D, the local electric potential ψ(x,t) and ion concentrations ci(x,t) and ion concentrations ci(x,t) in the electrolyte can be predicted using the modified Poisson-Nernst-Planck (MPNP) model given by

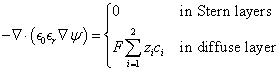
Conservation of energy shows that the local temperature T(r,t) is governed by the heat diffusion equation expressed as

with the local volumetric heat generation rate q̇(r,t). It can be divided into five contributions. The irreversible Joule heating is expressed as

where j and σ are the local current density vector and the local electrolyte conductivity, respectively given by

j = zF(N1-N2) and σ = Dz2F2(c1+c2)/RuT

The other four heat generation rates are reversible and equal to

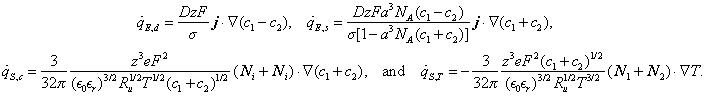
Physical interpretation

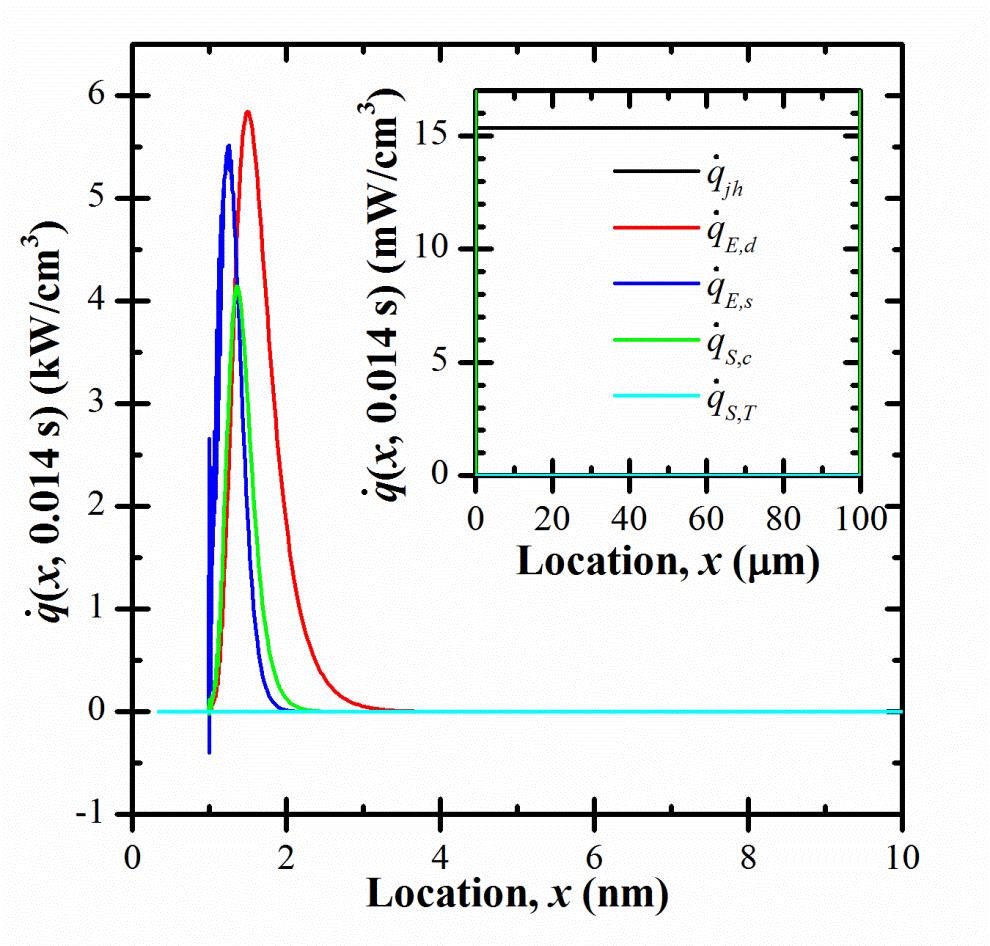
Three heat generation rates q̇E,j + q̇E,d + q̇E,s collectively represent the conversion of electrical energy into thermal energy. The irreversible Joule heat generation rate q̇E,j takes the same form as that in ohmic conductors, while the reversible heat generation rates q̇E,d and q̇E,s account for the effects of ion diffusion and steric effects, respectively. During the charging step, ions are driven into the EDLs by the electric field, decreasing their electrical potential energy and releasing thermal energy. During the discharging step, the ions were driven out of the EDLs by diffusion and steric effects, increasing their electrical potential energy and absorbing thermal energy.
Two heat generation rates q̇s,c and q̇s,T comprise the so-called heat of mixing. They represent the net heat generation rate due to ion fluxes along gradients of chemical potential, partial molar entropy, and temperature. The two heat generation rates and correspond to the heat of mixing heat generation rates arising from concentration gradients and from temperature gradients, respectively.

Results

Figure 1. Predicted heat generation rates as functions of location x at time t shortly before the end of a charging step under constant current js = 10 mA/cm2.

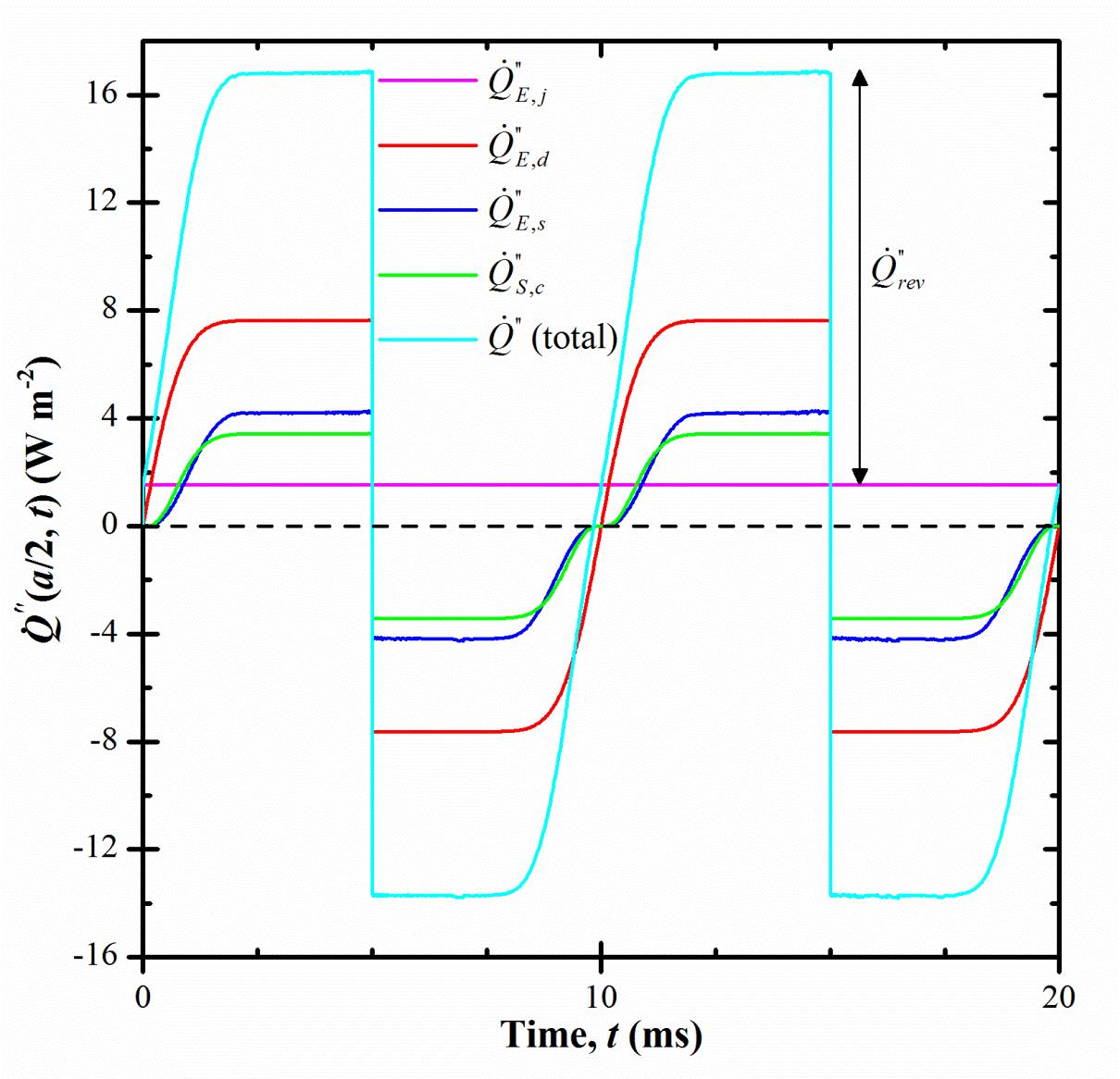
The overall heat generation rate throughout the electrolyte can be defined as

Figure 2. Predicted overall heat generation rates as well as the total heat generation rate as a function of time under current density js = 10 mA/cm2 and cycle period tc = 10 ms.

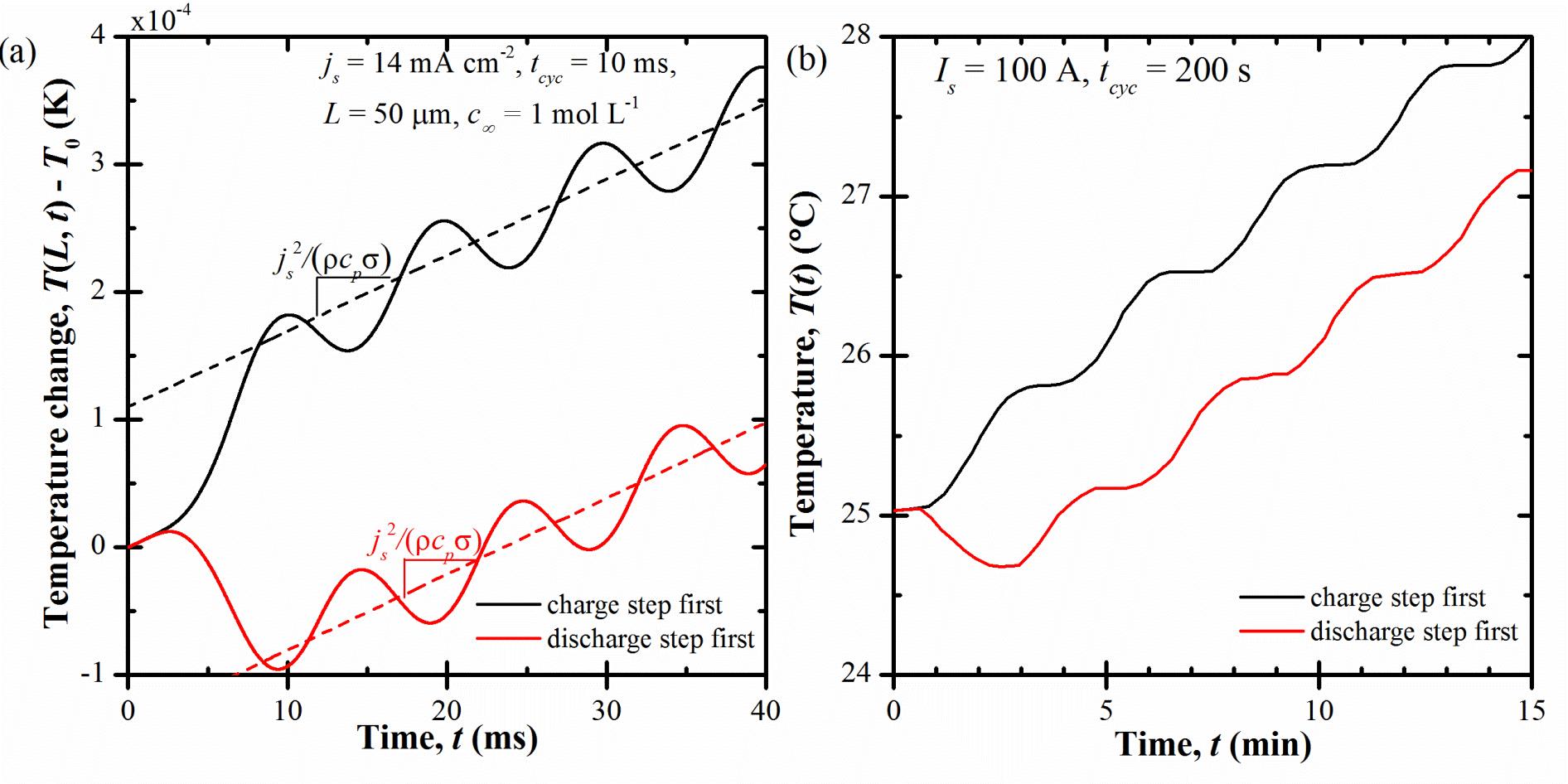
Figure 3. (a) Numerically predicted temperature change T(L,t)-T0 at the centerline and (b) measured surface temperature of a commercial EDLC (reproduced from Fig. 8 of Ref. [1]) as functions of time t for cases starting with either a charging step of a discharging step.

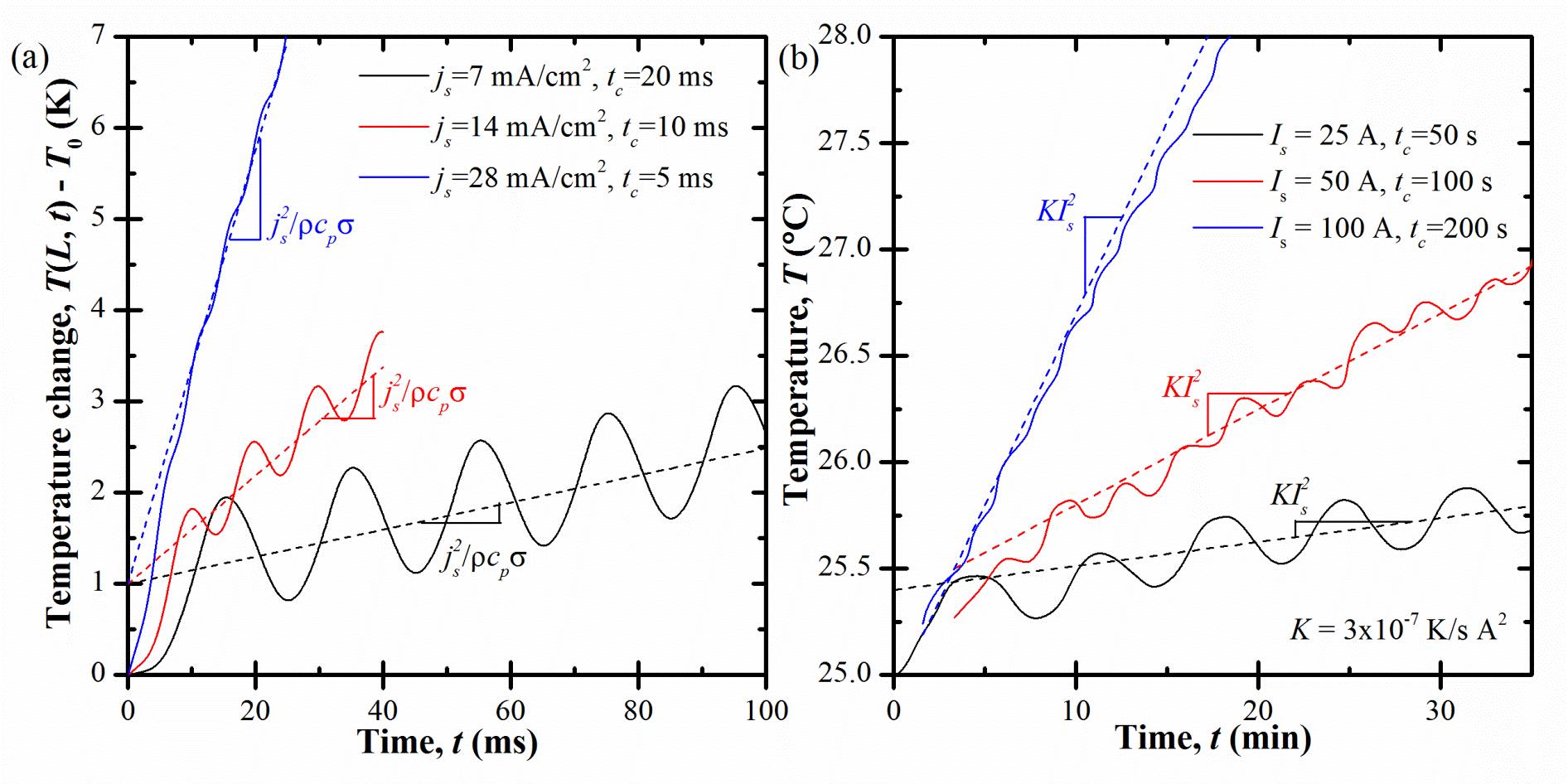
Figure 4.(a) Predicted temperature rise T(L,t)-T0 at the centerline for cycling at three different current densities jsover the same potential window and (b) measured surface temperature of a commercial EDLC during cycling under three different values of current Is over the same potential window (reproduced from Fig. 10 of Ref. [1]) as functions of time t.

Conclusions

This paper presented a new physical model for coupled ion transport and heat transfer during constant-current charging and discharging of EDLCs. The model accounted for the presence of the Stern layer and for the finite size of ions by using the modified Poisson-Nernst-Planck model. The new thermal model is important in that it predicts both the spatial and the temporal variations of the different heat generation rates and the temperature inside EDLCs based on first principles. Unlike previous thermal models, it accounted for the irreversible Joule heat generation rate as well as three reversible heat generation rates due to diffusion, steric effects, and entropy changes, respectively. To the best of our knowledge, the present study is the first to derive the diffusion and steric contributions to the heat generation in EDLCs. The reversible heat generation rates were exothermic during charging, endothermic during discharging, and localized in the EDLs. They resulted in large temperature oscillations near the electrodes with maximum temperatures significantly higher than those predicted by Joule heating alone. Predictions of temperature evolution were remarkably similar to those observed experimentally [1,2]. This indicates that the physical model developed captured the physical phenomena governing the thermal behavior of EDLCs.

References

[1] J. Schiffer, D. Linzen, D.U. Sauer, Journal of Power Sources 160 (2006) 765-772.
[2] H. Gualous, H. Louahlia, R. Gallay, IEEE Transactions on Power Electronics 26 (11) (2006) 3402-3409.

Publications

A.L. d'Entremont and L. Pilon, 2014. First Principles Thermal Modeling of Electric Double Layer Capacitors Under Constant-Current Cycling. Journal of Power Sources, Vol. 246, pp. 887- 898. doi:10.1016/j.jpowsour.2013.08.024 pdf

A.L. d’Entremont and L. Pilon, 2014. Scaling Laws For Heat Generation and Temperature Oscillations in EDLCs Under Galvanostatic Cycling. International Journal of Heat and Mass Transfer, Vol. 75, pp. 637–649. doi: 10.1016/j.ijheatmasstransfer.2014.04.001 pdf

A.L. d’Entremont, and L. Pilon, 2014. First-Order Thermal Model of Commercial EDLCs. Applied Thermal Engineering, Vol. 67, pp. 439-446. doi: 10.1016/j.applthermaleng.2014.03.061 pdf

A.L. d’Entremont and L. Pilon, 2015. Thermal Effects of Asymmetric Electrolytes in Electric Double Layer Capacitors. Journal of Power Sources, Vol. 273, pp. 196-209. doi. 10.1016/j.jpowsour.2014.09.080 pdf