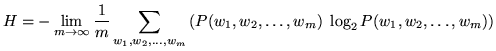Perplexity

A measure of language model performance based on average probability can be developed within the field of information theory [Shannon 1948]^14.16. A speaker emitting language can be considered to be a discrete information source which is generating a sequence of words $w_1, w_2, \ldots, w_m$ from a vocabulary set, $\mathbb{W}$. The probability of a symbol $w_i$ is dependent upon the previous symbols $w_1, \ldots, w_{i-1}$. The information source's inherent per-word entropy $H$ represents the amount of non-redundant information provided by each new word on average, defined in bits as:

$$H = - \lim_{m \to \infty} \frac{1}{m} \sum_{w_1, w_2, \ldots, w_m}\left( P(w_1, w_2, \ldots, w_m)\; \log_2 P(w_1, w_2, \ldots, w_m) \right)$$ (14.20)

This summation is over all possible sequences of words, but if the source is ergodic then the summation over all possible word sequences can be discarded and the equation becomes equivalent to:

$$H = - \lim_{m \to \infty} \frac{1}{m} \log_2 P(w_1, w_2, \ldots, w_m)$$ (14.21)

It is reasonable to assume ergodicity on the basis that we use language successfully without having been privy to all words that have ever been spoken or written, and we can disambiguate words on the basis of only the recent parts of a conversation or piece of text.

Having assumed this ergodic property, it follows that given a large enough value of $m$, $H$ can be approximated with:

$$\hat{H} = - \frac{1}{m} \log_2 P(w_1, w_2, \ldots, w_m)$$ (14.22)

This last estimate is feasible to evaluate, thus providing the basis for a metric suitable for assessing the performance of a language model.

Considering a language model as an information source, it follows that a language model which took advantage of all possible features of language to predict words would also achieve a per-word entropy of $H$. It therefore makes sense to use a measure related to entropy to assess the actual performance of a language model. Perplexity, $PP$, is one such measure that is in standard use, defined such that:

$$PP = 2^{\hat{H}}$$ (14.23)

Substituting equation 14.22 into equation 14.23 and rearranging obtains:

$$PP = \hat{P}(w_1, w_2, \ldots, w_m)^{-\frac{1}{m}}$$ (14.24)

where $\hat{P}(w_1, w_2, \ldots, w_m)$ is the probability estimate assigned to the word sequence $(w_1,$ $w_2,$ $\ldots, w_m)$ by a language model.

Perplexity can be considered to be a measure of on average how many different equally most probable words can follow any given word. Lower perplexities represent better language models, although this simply means that they `model language better', rather than necessarily work better in speech recognition systems - perplexity is only loosely correlated with performance in a speech recognition system since it has no ability to note the relevance of acoustically similar or dissimilar words.

In order to calculate perplexity both a language model and some test text are required, so a meaningful comparison between two language models on the basis of perplexity requires the same test text and word vocabulary set to have been used in both cases. The size of the vocabulary can easily be seen to be relevant because as its cardinality is reduced so the number of possible words given any history must monotonically decrease, therefore the probability estimates must on average increase and so the perplexity will decrease.