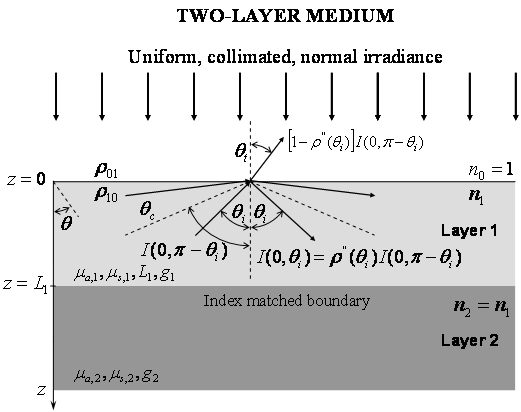
Diffuse reflectance spectroscopy consists of determining the radiative properties of an absorbing and scattering sample from diffuse reflectance measurements. It has been applied to noninvasive health-monitoring of in vivo biological tissues, quality control in agricultural applications, and remote terrestrial sensing, for example. In many biological applications, the irradiated medium can be modeled as a strongly scattering multilayer medium whose radiative properties are constant within each layer but differ from layer to layer. For example, the human cervix, colon, and skin have been modeled as two-layer optical systems. Skin consists of an outer layer called the epidermis and of an underlying layer called the dermis. The epidermis is characterized by strong absorption in the ultraviolet and visible part of the spectrum due to melanin. On the other hand, the blood and connective tissues are responsible for absorption and scattering in the dermis. In addition, the absorption characteristics of blood depend on the concentrations of oxyhemoglobin and deoxyhemoglobin.
The objective of this study is to develop simple and accurate expressions for the diffuse reflectance of semi-infinite and two-layer absorbing and scattering media. Such expressions could be combined with an inverse method to retrieve the radiation properties and thickness of these media based on spectral diffuse reflectance measurements.
Simple analytical expressions for the diffuse reflectance of the semi-infinite and two-layer media considered were first derived using the two flux approximation. Then, parameters appearing in the analytical expression previously derived were instead fitted to match results from more accurate Monte Carlo simulations. A single semiempirical parameter was sufficient to relate the diffuse reflectance to the radiative properties and thickness of the semiinfinite and two-layer media. All media were assumed to be nonemitting, strongly forward scattering. The incident light source was a collimated, monochromatic, and normally incident beam of infinite radius.
Semi-Infinite Medium
Two-Layer Medium

The semi-empirical model describing reflectance from a single layer system was given by
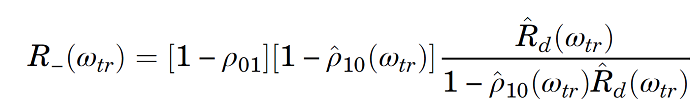
where the reflectivity at the medium/air interface accounting for the fact that intensity inside the medium
is not diffusely incident on the medium/air interface:
![]()
The approximate diffuse reflectance was approximated
![]()
where the values of Ai and Bi for N=3 can be found in Ref. [1].
![]()
where R- is given above and R* is
![]()
Here, Y1 is the optical thickness parameter of Layer 1. The parameter α was found empirically and given for various values of n1 in the figure below.
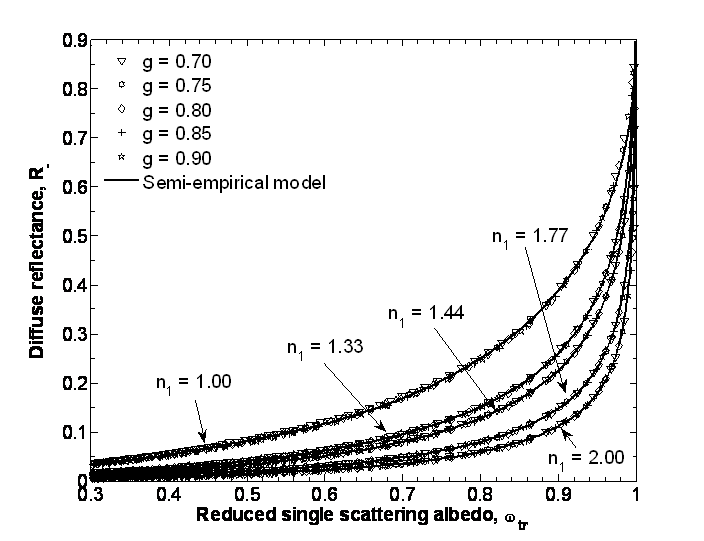
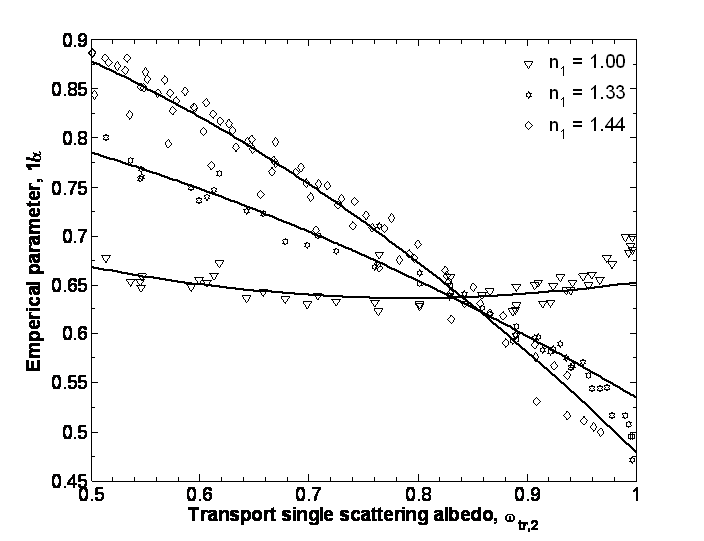
Conclusions
We presented computationally efficient and accurate semiempirical models of light transfer suitable for real-time diffuse reflectance spectroscopy. The models predict the diffuse reflectance of both (i) semiinfinite homogeneous and (ii) two-layer media exposed to normal and collimated light. The two-layer medium consisted of a plane-parallel slab of finite thickness over a semi-infinite layer with identical index of refraction but different absorption and scattering properties. The model accounted for absorption and anisotropic scattering, as well as for internal reflection at the medium/air interface. The present model can be used for a wide range of applications including noninvasive diagnosis of biological tissue.
Publications
D. Yudovsky, A. Nouvong, K. Schomacker, and L. Pilon, 2011. Monitoring Temporal Development and Healing of Diabetic Foot Ulcer Using Hyperspectral Imaging, Journal of Biophotonics, Vol. 4, No. 7-8, pp. 565-576. doi:10.1002/jbio.201000117 pdf
D. Yudovsky and L. Pilon, 2011. Retrieving Skin Properties From In Vivo Diffuse Reflectance Measurements on Human Skin, Journal of Biophotonics, Vol. 4, No.5, pp.305-314, doi:10.1002/jbio.201000069 pdf
D. Yudovsky, A. Nouvong, K. Schomacker, and L. Pilon, 2011. Assessing Diabetic Foot Ulcer Development Risk with Hyperspectral Tissue Oximetry, Journal of Biomedical Optics, Vol.16, No.2, 026009. doi: doi:10.1117/1.3535592 pdf
D. Yudovsky and L. Pilon, 2010. Modeling of Local Excitation Fluence Rate and Florescence Emission in Absorbing and Strongly Scattering Multilayered Media. Applied Optics, Vol. 49, No. 31, pp. 6072-6084. doi:10.1364/AO.49.006072 pdf
D. Yudovsky , A. Nouvong, and L. Pilon, 2010. Hyperspectral Imaging for Diabetic Foot Wound Care, Journal of Diabetes Science and Technology, Vol.4, No.5, pp. 1099-1113. pdf