CSL Home
NSF Feedback Project
Publications
Research
Group
Research
Interests
Research
Opportunities
Sponsors
Contact

Overview of Feedback-related Research
“Can you send me some papers about feedback?”, a newcomer to the research group might ask. Other common questions related to our research are “What is incremental redundancy?”, “What do you mean by punctured codes?”, and “How does this relate to finite-blocklength information theory?”

This page attempts to answer those questions and provide an overview of the classic and recent literature related to our feedback research efforts. “Feedback” in this context spans several areas of communications, coding, and information theory. Please contact the webmaster if you have suggestions for recommended additions to this page.

Contents

Puncturing (and Rate-compatible Puncturing)
Incremental Redundancy
Hybrid ARQ
Finite-blocklength Information Theory
Low-latency Coding
Reliability-based Decoding Algorithms
What Kind of Feedback?

Puncturing (and Rate-compatible Puncturing)

A classic paper that illustrates the puncturing concept is by Hagenauer in 1988. In punctured codes, a low-rate codeword of N symbols is generated by the encoder, but only a portion of the coded symbols are transmitted. The missing symbols are called “punctured”, and the receiver decodes without the full codeword.
  • J. Hagenauer, “Rate-compatible punctured convolutional codes (RCPC codes) and their applications,” IEEE Trans. Commun., vol. 36, no. 4, pp. 389–400, Apr. 1988.
Punctured codes can be used in communication systems with a rate-adaption mechanism. When the signal-to-noise ratio (SNR) is high, high-rate codewords can be sent and decoded reliably, but when the SNR is low, low-rate codewords can be sent to increase the reliability. Puncturing is common for both convolutional codes as well as low-density parity-check (LDPC) block codes.

More germane to our research are rate-compatible punctured codes, which is a family of punctured codes with various rates. In rate-compatible codes, all code bits of a high-rate code are also used by the lower-rate codes. These codes are suitable for use in an incremental redundancy scheme.
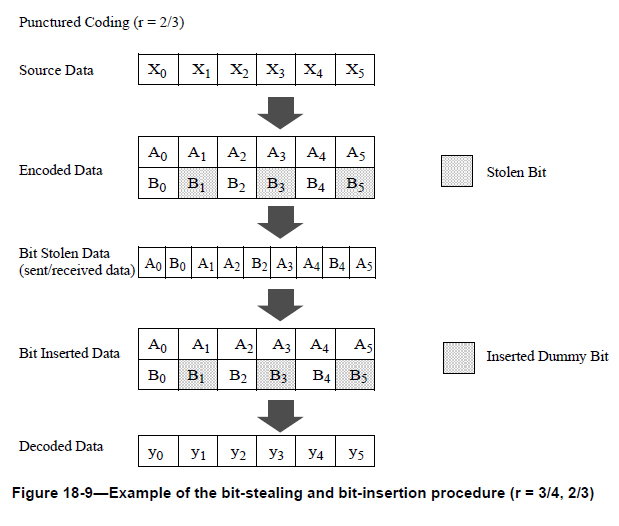
The figure above shows an example of the puncturing matrix used in the IEEE 802.11 wireless standard. Rate 1/2 mother codes are punctured to generate rate 2/3 codes.

Incremental Redundancy

In Automatic Repeat reQuest (ARQ) schemes, the receiver uses feedback to tell the transmitter whether it has decoded correctly (often called an ACK for acknowledgement) or not (negative acknowledgement, or NACK). The transmitter will then repeat by sending the same block over again. This continues until the receiver has decoded successfully.

First used by Mandelbaum in 1974, the term incremental redundancy refers to a decision–feedback scheme in which the transmitter only has to send additional coded increments after the receiver fails to decode, instead of sending the entire block. After each transmission, the receiver will attempt to decode with all the received blocks, not just the last increments. With rate-compatible codes, a single encoder can be used to generate a sequence of high-rate to low-rate codewords.
  • D. Mandelbaum, “An adaptive-feedback coding scheme using incremental redundancy (corresp.),” IEEE Trans. Inf. Theory, vol. 20, no. 3, pp.388 – 389, May 1974.
Typically, there would be a maximum m number of increments before the transmitter would start over with the first block or give up and move on to the next message. The figure below illustrates an example of the m increments, with length I_1, I_2, I_3, …, I_m. After receiving each increment I_i, the receiver attempts to decode with N_i = I_1 + … + I_i symbols. If the number of message bits is k, this means that the instantaneous rate at the ith decoding attempt is R_i = k / N_i. Often, the size of the first increment I_1 is larger than the subsequent increments, since the initial blocklength needs to be long enough to achieve a reasonably small error-probability.


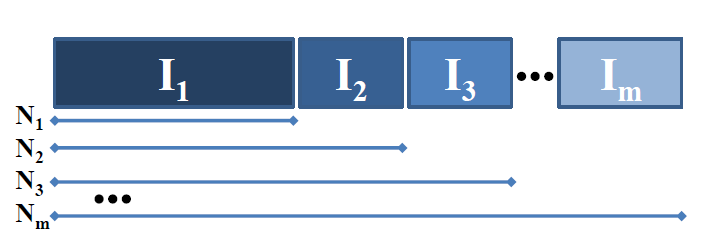
There are many papers discussing incremental redundancy schemes, both in the communications and information theory literature, including several papers from our group. A good starting point is the following paper by Williamson, Chen, and Wesel, which provides equations for computing the average throughput (coding rate) and latency (blocklength) of incremental redundancy systems.

Hybrid ARQ

The original instances of ARQ systems transmitted uncoded data bits along with parity bits from an error-detection code, such as a cyclic redundancy check (CRC). The ACK/NACK requests from the receiver were determined by the result of the CRC. Later, error-correction codes (also called forward error-correction) were used to in order to communicate more reliably. The combination of ARQ error-control and error-correction codes became known as hybrid ARQ (HARQ).

A good reference for hybrid ARQ and incremental redundancy is the work of Emina Soljanin at Bell Labs, whose research includes LDPC and Raptor codes in the context of HARQ: Over time, different variants of hybrid ARQ have been labeled as type-I, type-II, and type-III hybrid ARQ, though these names can sometimes mean different things. In our research, we use the name type-I HARQ to refer to coded systems with only 1 possible blocklength (m=1), in which the same block is repeated on each retransmission. Type-II HARQ refers to incremental redundancy systems described above (m>1), in which the smaller increments are transmitted and the receiver decodes with all received symbols. Finally, type-III HARQ refers to self-decodable packets, suitable for fading channels. That is, if the first block is decoded in error due to a deep fade (low SNR), the second block must be able to be decoded on its own and cannot be just a short increment. In type-III HARQ systems, each of the m transmissions lengths are typically the same.

The following paper also describes the different types of hybrid ARQ:
  • T.-Y. Chen, A. R. Williamson, and R. D. Wesel, “Feedback communication systems with limitations on incremental redundancy,” submitted to IEEE Trans. Inf. Theory.
    http://arxiv.org/abs/1309.0707
When transmitted symbols are repeated, the receiver may discard the previously received symbols, or it may use maximum-ratio combining to effectively increase the received SNR. This is called Chase combining, named after an early paper by Chase. Incremental redundancy has been shown to deliver higher rates than Chase combining alone. In practical systems, larger buffer sizes are needed to manage the received increments.
  • Chase, D., "Code Combining – A maximum-likelihood decoding approach for combining an arbitrary number of noisy packets," IEEE Trans. Commun., vol.33, no.5, pp.385-393, May 1985.

Finite-blocklength Information Theory

Shannon showed in 1956 that noiseless feedback does not increase the capacity of memoryless channels, at least when the blocklength of a code is allowed to go to infinity. That is, asymptotically, the capacity is the same regardless of whether feedback is used.
  • C. E. Shannon, “The zero error capacity of a noisy channel,” IRE Trans. Inf. Theory, vol. 2, no. 3, pp. 8–19, Sep. 1956.
However, researchers have known for some time that feedback is still beneficial. Feedback can improve the error exponent (how quickly the error probability decays with increasing blocklength) and may simplify encoding and decoding operations.

Shannon’s asymptotic definition of a channel’s capacity may seem problematic (since no code used in the real world can have an infinite length!), yet this definition of channel capacity has proved extremely useful in the real world. It has helped researchers design error-correcting codes and measure their performance relative to the maximum coding rate (the capacity).

Still, even in the 1960s, Shannon and his contemporaries investigated the finite-length performance of codes, evaluating the achievable rates and error probabilities of codes with practical lengths. Activity in this field diminished over time, but a seminal paper of Polyanskiy, Poor, and Verdú in 2010 quickly sparked a resurgence in this area. Polyanskiy et al. provided new bounds on the maximum rate achievable at fixed blocklengths and error probabilities. Their work was focused on point-to-point, static channels, though other researchers have extended their ideas to analyze multi-user channels and fading channels.
  • Y. Polyanskiy, H. V. Poor, and S. Verdú, “Channel coding rate in the finite blocklength regime,” IEEE Trans. Inf. Theory, vol. 56, no. 5, pp.2307–2359, May 2010.
    http://people.lids.mit.edu/yp/homepage/
Polyanskiy, Poor, and Verdú’s 2010 paper dealt mainly with fixed-length codes without feedback, showing that there is a severe backoff from capacity at short blocklengths (for example, under 100 bits). A 2011 paper by the same team provided new guidance on the maximum rate achievable when feedback is present, showing that feedback can significantly improve the finite-blocklength rate.
  • Y. Polyanskiy, H. V. Poor, and S. Verdú, “Feedback in the non-asymptotic regime,” IEEE Trans. Inf. Theory, vol. 57, no. 8, pp. 4903–4925, Aug. 2011.
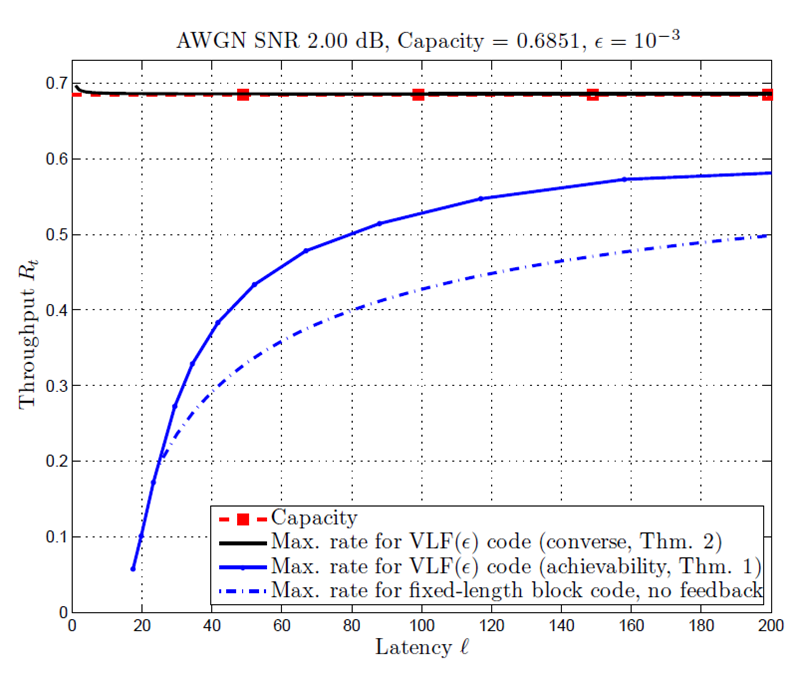
They coined the term variable-length feedback (VLF) codes to describe a transmission scheme in which the receiver can decide to stop decoding after any received symbol. In this framework, the length of the code is not fixed but a random variable, and the rate is computed by taking an expectation over the random stopping time. The figure below shows the upper (converse) and lower (achievability) bounds on rate for VLF codes on the AWGN channel. The no-feedback curve uses Polyanskiy, Poor, and Verdú's normal approximation, which is based on the channel dispersion.
In this light, incremental redundancy schemes (hybrid ARQ) are a special case of VLF codes. Instead of being able to stop transmission after any received symbol, however, hybrid ARQ systems in practice limit decoding to one of several possible blocklengths. As a result, the VLF results of Polyanskiy, Poor, and Verdú provide a helpful information-theoretic benchmark to see how well incremental redundancy schemes perform in the short-blocklength regime. Chen, Williamson, and Wesel have extended the VLF analysis of Polyanskiy et al. to include practical limitations on decoding lengths.
  • T.-Y. Chen, A. R. Williamson, and R. D. Wesel, “Variable-length coding with feedback: Finite-length codewords and periodic decoding,” in Proc. 2013 IEEE Int. Symp. Inf. Theory (ISIT), Istanbul, Turkey, July 2013.
    http://arxiv.org/abs/1301.7464
Polyanskiy et al.’s results were general in that they applied to any discrete memoryless channel and that the analysis was independent of any particular code. Instead, the lower bound on code rate was derived by analyzing an ensemble of random codes. Williamson, Chen, and Wesel have shown that convolutional codes could deliver an average rate above the random coding lower bounds of Polyanskiy et al., in several different VLF configurations.
  • A. R. Williamson, T.-Y. Chen, and R. D. Wesel, “Reliability-based error detection for feedback communication with low latency," in Proc. 2013 IEEE Int. Symp. Inf. Theory (ISIT), Istanbul, Turkey, July 2013.
    http://arxiv.org/abs/1305.4560
  • A. R. Williamson, T.-Y. Chen, and R. D. Wesel, “Firing the genie: Two-phase short-blocklength convolutional coding with feedback," in 2013 Inf. Theory and Applications Workshop (ITA), Feb. 2013.
    http://ita.ucsd.edu/workshop/13/files/paper/paper_293.pdf

Low-latency Coding

Convolutional codes are not capacity-approaching, unlike turbo codes and LDPC codes. However, their performance at short blocklengths can often surpass that of capacity-approaching codes. This benefit motivated our use of punctured convolutional codes in feedback systems.

Recent research has also compared the short-blocklength performance of convolutional codes (with maximum-likelihood, Viterbi decoding) to LDPC codes (with iterative message-passing decoding) and convolutional codes (with stack sequential decoding). Maiya, Costello, and Fuja found that for a fixed target error-rate (e.g., BER = 10-6) and code rate (e.g., Rc = 1/2 ), Viterbi-decoded convolutional codes offered the best performance at low latency (e.g., less than 100 bits) and that LDPC codes decoded with iterative message passing offered the best performance for high latencies (e.g., greater than 220 bits). In an intermediate range of latencies (e.g., 100 to 220 bits), convolutional codes with stack sequential decoding were optimal.
  • S. V. Maiya, D. J. Costello, Jr., and T. E. Fuja, “Low latency coding:Convolutional codes vs. LDPC codes,” IEEE Trans. Commun., vol. 60, no. 5, pp. 1215–1225, May 2012.
    http://www3.nd.edu/~eecoding/Welcome.html

Reliability-based Decoding Algorithms

In order for the receiver in a feedback-based retransmission scheme to request additional symbols, the receiver must decide whether the received word is reliable. Two common methods are CRCs, also called the code-based approach, and reliability-based decoding.

CRCs are commonly used to detect errors in modern wired and wireless communications systems. If the check bits computed by the decoder do not match the received check bits, additional symbols are requested. However, undetected errors can occur when the check bits erroneously match. For more information about choosing the appropriate CRC polynomials (and to see how some CRCs in standards are not optimal), consult the excellent work of Koopman at Carnegie Mellon:
  • P. Koopman and T. Chakravarty, “Cyclic redundancy code (CRC) polynomial selection for embedded networks,” in 2004 IEEE Int. Conf. Dependabl Systems and Networks (DSN), July 2004, pp. 145 – 154.
    http://www.ece.cmu.edu/~koopman/projects.html#crc
Due to the overhead of transmitting the CRC bits in this code-based approach, there is also a rate loss that can be especially significant at short blocklengths. For this reason, reliability-based decoding may be preferred. Instead of making a binary decision on the decoded word (for example, it passes or fails the CRC), reliability-based decoders compute a soft metric.
Many reliability-based decoding algorithms have been designed for convolutional codes that take advantage of the trellis structure, which makes the complexity manageable. Two salient examples are the Yamamoto-Itoh algorithm and Raghavan and Baum’s reliability-output Viterbi algorithm (ROVA). The ROVA computes the exact word-error probability of a a decoded word given the received sequence, 1 – P(x|y). The Yamamoto-Itoh algorithm does not compute the exact word-error probability, but similarly determines whether the surviving path in a Viterbi decoder is sufficiently reliable, based on a reliability parameter.
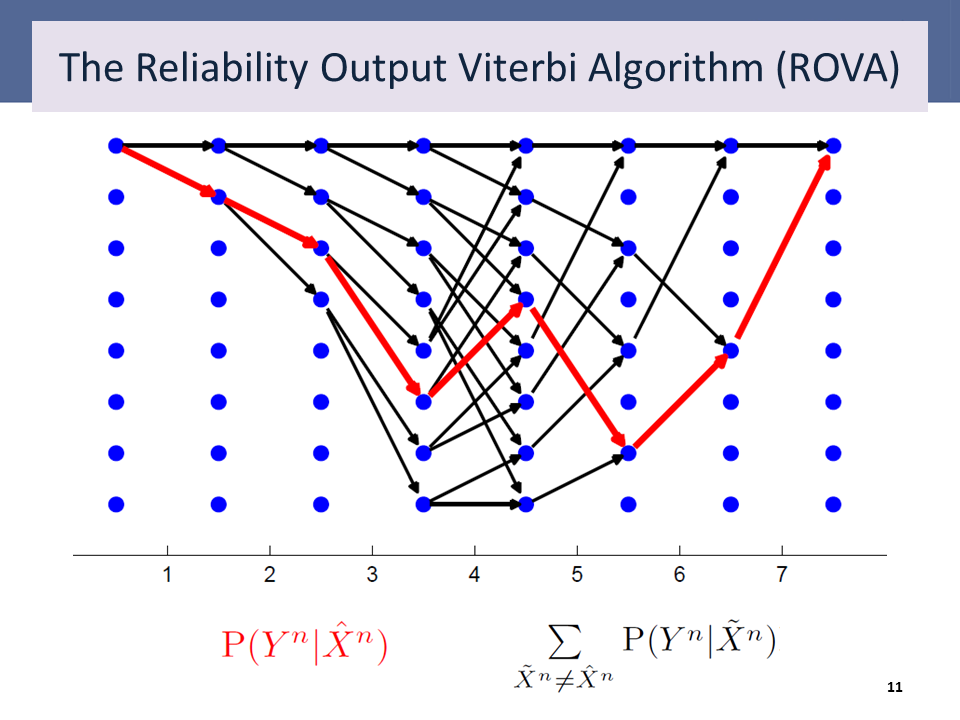
  • A. Raghavan and C. Baum, “A reliability output Viterbi algorithm with applications to hybrid ARQ,” IEEE Trans. Inf. Theory, vol. 44, no. 3, pp. 1214–1216, May 1998.
  • H. Yamamoto and K. Itoh, “Viterbi decoding algorithm for convolutional codes with repeat request,” IEEE Trans. Inf. Theory, vol. 26, no. 5, pp. 540–547, Sep. 1980.
Both of these algorithms have been used in a number of repeat request schemes (that is, ARQ or HARQ). Fricke and Hoeher compared the throughputs of the reliability-based error detection approach using the ROVA and the code-based approach using CRCs.
  • J. Fricke and P. Hoeher, “Reliability-based retransmission criteria for hybrid ARQ,” IEEE Trans. Commun., vol. 57, no. 8, pp. 2181–2184, Aug. 2009.
There have also several extensions to and variations of these algorithms. Fricke and Hoeher provided a simplified version of the ROVA that significantly decreases the complexity of the word-error computations, in exchange for approximating the desired probability.
  • J. Fricke and P. Hoeher, “Word error probability estimation by means of a modified Viterbi decoder,” in Proc. 66th IEEE Veh. Technol. Conf. (VTC), Oct. 2007, pp. 1113–1116.
In a 2009 paper, Hof, Sason, and Shamai presented an augmented Viterbi algorithm that permits reliability-based decoding according to Forney’s generalized decoding rule. Generalized decoding is a framework that allows the decoder to select either the maximum-likelihood (ML) codeword, to specify a list of the most likely codewords, or to declare an erasure, based on the value of a generalized decoding parameter. When the parameter is selected for ML decoding with erasures, Hof et al.’s algorithm is equivalent to the ROVA.
  • E. Hof, I. Sason, and S. Shamai (Shitz), “On Optimal Erasure and List Decoding Schemes of Convolutional Codes,” in Proc. Tenth Int. Symp. Commun. Theory and Applications (ISCTA), July 2009, pp. 6–10.
  • G. Forney, “Exponential error bounds for erasure, list, and decision feedback schemes,” IEEE Trans. Inf. Theory, vol. 14, no. 2, pp. 206–220, Mar. 1968.
Hashimoto has several good papers explaining Forney’s optimal decision rule and comparing it to other suboptimal decision rules in terms of the error exponents. Forney's rule may be computationally prohibitive, since it requires the decoder to compute the likelihood of all 2^k codewords, so reduced-complexity, suboptimal rules can be preferred in practice. The following paper makes connections to Raghavan and Baum’s ROVA and the Yamamoto-Itoh algorithm.
  • T. Hashimoto, "Composite scheme LR+Th for decoding with erasures and its effective equivalence to Forney's rule," IEEE Trans. Inf. Theory, vol.45, no.1, pp.78,93, Jan 1999.

What Kind of Feedback?

Our research assumes that noiseless feedback is sent from the receiver to the transmitter after each forward channel use. The variable-length feedback coding framework of Polyanskiy, Poor, and Verdú allows for a full-precision version of the nth received symbol y_n to be fed back, which the transmitter may use to select the subsequent transmitted symbol x_{n+1}.

In many practical cases, however, feedback is only used to inform the transmitter whether the receiver has finished decoding (ACK) or needs additional symbols (NACK). Polyanskiy, Poor, and Verdú refer to this as a stop-feedback code, since feedback is used by the transmitter to learn when the receiver stops. Forney calls this decision feedback, indicating that the receiver sends back its decision, but not the received symbols. In these cases, only 1 bit of feedback (still noiseless) is required. While in practice no transmissions can be entirely noise-free, the noiseless assumption seems reasonable, since the 1 bit could be sufficiently protected with a low-rate code.

In contrast, Forney refers to systems in which the receiver sends back the received symbols as information feedback. This paradigm allows the transmitter to adapt its future coded symbols based on the information received so far. Recent work by Naghshvar and Javidi generalizes this setup as active, sequential hypothesis-testing, of which channel coding is just one example. The variable-length aspect of feedback coding explains the “sequential” descriptor, and “active” indicates that the codebook is not generated before message transmission, but that coded symbols are generated progressively, as a result of the feedback messages. Active, sequential hypothesis-testing is a big change for information theorists, since familiar random-coding proofs cannot be applied. Codebooks in the traditional sense do not exist, since the coded symbols corresponding to a particular message will not be known at the transmitter until it has gotten feedback of the previous channel outputs from the receiver. Even so, Naghshvar and Javidi have shown that active, sequential hypothesis-testing can achieve Burnashev's optimal error-exponent for codes with feedback.

There are opportunities to use the ideas of active feedback for short-blocklength codes, as well. In the following paper, Williamson, Chen, and Wesel constructed a two-phase scheme that uses feedback to confirm or deny the receiver's tentative estimate. We showed that this communication and confirmation scheme, inspired by the classical error-exponent papers, could beat the random-coding lower bound for VLF codes. We used convolutional codes in the communication phase and repetition codes in the confirmation phase.
Files (top)
  • en_US.dic: a custom LaTeX dictionary file to aid in spellchecking. It includes common nouns and proper nouns prominent in the information theory literature, such as "non-asymptotic", "achievability", and "Burnashev". This will eliminate unnecessary red-underlining in your TeX editor. It can also be used with Evernote and other programs that use dictionary files. On my Windows computer, the directory this should be placed in is:
    C:\Users\[USERNAME]\TeXworks\dictionaries
This material is based upon work supported by the National Science Foundation under Grant Number 1162501. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
  Copyright@2007-2013 UCLA CSL