The HMM Definition Language

To conclude this chapter, this section presents a formal description of the HMM definition language used by HTK. Syntax is described using an extended BNF notation in which alternatives are separated by a vertical bar $ \vert$, parentheses () denote factoring, brackets [ ] denote options, and braces {} denote zero or more repetitions.

All keywords are enclosed in angle brackets7.7 and the case of the keyword name is not significant. White space is not significant except within double-quoted strings.

The top level structure of a HMM definition is shown by the following rule. 


		  hmmdef = 		 [ $ \sim$h macro ] 

$ <$BeginHMM$ >$ 


$ <$NumStates$ >$ short 


state { state } 


transP 


$ <$EndHMM$ >$
A HMM definition consists of an optional set of global options followed by the $ <$NumStates$ >$ keyword whose following argument specifies the number of states in the model inclusive of the non-emitting entry and exit states7.8. The information for each state is then given in turn, followed by the parameters of the transition matrix and the model duration parameters, if any. The name of the HMM is given by the $ \sim$h macro. If the HMM is the only definition within a file, the $ \sim$h macro name can be omitted and the HMM name is assumed to be the same as the file name.

The global options are common to all HMMs. They can be given separately using a $ \sim$o option macro 


		 optmacro = 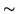		 $ \sim$o globalOpts
or they can be included in one or more HMM definitions. Global options may be repeated but no definition can change a previous definition. All global options must be defined before any other macro definition is processed. In practice this means that any HMM system which uses parameter tying must have a $ \sim$o option macro at the head of the first macro file processed.

The full set of global options is given below. Every HMM set must define the vector size (via $ <$VecSize$ >$), the stream widths (via $ <$StreamInfo$ >$) and the observation parameter kind. However, if only the stream widths are given, then the vector size will be inferred. If only the vector size is given, then a single stream of identical width will be assumed. All other options default to null. 


		 globalOpts = 		 option { option } 


option = 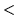		 $ <$HmmSetId$ >$ string $ \vert$ 

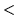$ <$StreamInfo$ >$ short { short } $ \vert$ 

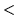$ <$VecSize$ >$ short $ \vert$ 

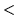$ <$ProjSize$ >$ short $ \vert$ 

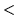$ <$InputXform$ >$ inputXform $ \vert$ 

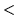$ <$ParentXform$ >$ $ \sim$a macro $ \vert$ 


covkind $ \vert$ 


durkind $ \vert$ 


parmkind
The $ <$HmmSetId$ >$ option allows the user to give the MMF an identifier. This is used as a sanity check to make sure that a TMF can be safely applied to this MMF. The arguments to the $ <$StreamInfo$ >$ option are the number of streams (default 1) and then for each stream, the width of that stream. The $ <$VecSize$ >$ option gives the total number of elements in each input vector. $ <$ProjSize$ >$ is the number of ``nuisance'' dimensions removed using, for example, an HLDA transform. The $ <$ParentXForm$ >$ allows the semi-tied macro, if any, associated with the model-set to be specified. If both $ <$VecSize$ >$ and $ <$StreamInfo$ >$ are included then the sum of all the stream widths must equal the input vector size.

The covkind defines the kind of the covariance matrix 


		  covkind=		 $ <$DiagC$ >$ $ \vert$ $ <$InvDiagC$ >$ $ \vert$ $ <$FullC$ >$ $ \vert$ 

$ <$LLTC$ >$ $ \vert$ $ <$XformC$ >$
where $ <$InvDiagC$ >$ is used internally. $ <$LLTC$ >$ and $ <$XformC$ >$ are not used in HTK Version 3.4. Setting the covariance kind as a global option forces all components to have this kind. In particular, it prevents mixing full and diagonal covariances within a HMM set.

The durkind denotes the type of duration model used according to the following rules 


		  durkind=		 $ <$nullD$ >$ $ \vert$ $ <$poissonD$ >$ $ \vert$ $ <$gammaD$ >$ $ \vert$ $ <$genD$ >$
For anything other than $ <$nullD$ >$, a duration vector must be supplied for the model or each state as described below. Note that no current HTK tool can estimate or use such duration vectors.

The parameter kind is any legal parameter kind including qualified forms (see section 5.1) 


		  parmkind=		 $ <$basekind{_D$ \vert$_A$ \vert$_T$ \vert$_E$ \vert$_N$ \vert$_Z$ \vert$_O$ \vert$_V$ \vert$_C$ \vert$_K}$ >$ 


basekind=		 $ <$discrete$ >$$ \vert$$ <$lpc$ >$$ \vert$$ <$lpcepstra$ >$$ \vert$$ <$mfcc$ >$ $ \vert$ $ <$fbank$ >$ $ \vert$ 

$ <$melspec$ >$$ \vert$ $ <$lprefc$ >$$ \vert$$ <$lpdelcep$ >$ $ \vert$ $ <$user$ >$
where the syntax rule for parmkind is non-standard in that no spaces are allowed between the base kind and any subsequent qualifiers. As noted in chapter 5, $ <$lpdelcep$ >$ is provided only for compatibility with earlier versions of HTK and its further use should be avoided.

Each state of each HMM must have its own section defining the parameters associated with that state 


		 state=		  $ <$State: Exp $ >$ short stateinfo
where the short following $ <$State: Exp $ >$ is the state number. State information can be defined in any order. The syntax is as follows 

		   stateinfo = 		 $ \sim$s macro $ \vert$ 
[ weights ] stream { stream } [ duration ] 


macro     = 		 string
A stateinfo definition consists of an optional specification of the number of mixture components, an optional set of stream weights, followed by a block of information for each stream, optionally terminated with a duration vector. Alternatively, $ \sim$s macro can be written where macro is the name of a previously defined macro.

The optional mixes in a stateinfo definition specify the number of mixture components (or discrete codebook size) for each stream of that state 


		   mixes = 		  $ <$NumMixes$ >$ short {short}
where there should be one short for each stream. If this specification is omitted, it is assumed that all streams have just one mixture component.

The optional weights in a stateinfo definition define a set of exponent weights for each independent data stream. The syntax is 


		   weights = 		 $ \sim$w macro $ \vert$ $ <$SWeights$ >$ short vector 


vector  = 		 float { float }
where the short gives the number $ S$ of weights (which should match the value given in the $ <$StreamInfo$ >$ option) and the vector contains the $ S$ stream weights $ \gamma_s$ (see section 7.1).

The definition of each stream depends on the kind of HMM set. In the normal case, it consists of a sequence of mixture component definitions optionally preceded by the stream number. If the stream number is omitted then it is assumed to be 1. For tied-mixture and discrete HMM sets, special forms are used. 


		   stream = 		 [ $ <$Stream$ >$ short ] 

(mixture { mixture } $ \vert$ tmixpdf $ \vert$ discpdf)

The definition of each mixture component consists of a Gaussian pdf optionally preceded by the mixture number and its weight 


		   mixture = 		 [ $ <$Mixture$ >$ short float ] mixpdf
If the $ <$Mixture$ >$ part is missing then mixture 1 is assumed and the weight defaults to 1.0.

The tmixpdf option is used only for fully tied mixture sets. Since the mixpdf parts are all macros in a tied mixture system and since they are identical for every stream and state, it is only necessary to know the mixture weights. The tmixpdf syntax allows these to be specified in the following compact form 


		   tmixpdf = 		 $ <$TMix$ >$ macro weightList 


weightList = 		 repShort { repShort } 


repShort = 		 short [ $ \ast$ char ]
where each short is a mixture component weight scaled so that a weight of 1.0 is represented by the integer 32767. The optional asterix followed by a char is used to indicate a repeat count. For example, 0*5 is equivalent to 5 zeroes. The Gaussians which make-up the pool of tied-mixtures are defined using $ \sim$m macros called macro1, macro2, macro3, etc.

Discrete probability HMMs are defined in a similar way 


		   discpdf = 		 $ <$DProb$ >$ weightList
The only difference is that the weights in the weightList are scaled log probabilities as defined in section 7.6.

The definition of a Gaussian pdf requires the mean vector to be given and one of the possible forms of covariance 


		   mixpdf = 		 $ \sim$m macro $ \vert$ mean cov [ $ <$GConst$ >$ float ] 


mean = 		 $ \sim$u macro $ \vert$ $ <$Mean$ >$ short vector 


cov = 		 var $ \vert$ inv $ \vert$ xform 


var = 		 $ \sim$v macro $ \vert$ $ <$Variance$ >$ short vector 


inv = 		 $ \sim$i macro $ \vert$ 

($ <$InvCovar$ >$ $ \vert$ $ <$LLTCovar$ >$) short tmatrix 


xform = 		 $ \sim$x macro $ \vert$ $ <$Xform$ >$ short short matrix 


matrix = 		 float {float} 


tmatrix = 		 matrix
In mean and var, the short preceding the vector defines the length of the vector, in inv the short preceding the tmatrix gives the size of this square upper triangular matrix, and in xform the two short's preceding the matrix give the number of rows and columns. The optional $ <$GConst$ >$7.9 gives that part of the log probability of a Gaussian that can be precomputed. If it is omitted, then it will be computed during load-in, including it simply saves some time. HTK tools which output HMM definitions always include this field.

In addition to defining the output distributions, a state can have a duration probability distribution defined for it. However, no current HTK tool can estimate or use these. 


		   duration = 		 $ \sim$d macro $ \vert$ $ <$Duration$ >$ short vector
Alternatively, as shown by the top level syntax for a hmmdef, duration parameters can be specified for a whole model.

The transition matrix is defined by 


		   transP = 		 $ \sim$t macro $ \vert$ $ <$TransP$ >$ short matrix
where the short in this case should be equal to the number of states in the model.

To support HMM adaptation (as described in chapter 9) baseclasses and regression class trees are defined. A baseclass is defined as 


		   baseClass = 		 $ \sim$b macro  baseopts classes


baseopts  = 		 $ <$MMFIdMask$ >$ string $ <$Parameters$ >$ baseKind $ <$NumClasses$ >$ int


baseKind  = 		MIXBASE $ \vert$ MEANBASE $ \vert$ COVBASE 


classes   = 		 $ <$Class$ >$ int itemlist  { classes }
where itemlist is a list of mixture components specified using the same conventions as the HHED command described in section 10.3. A regression class tree may also exist for an HMM set. This is defined by 

		   regTree = 		 $ \sim$r macro $ <$BaseClass$ >$ baseclasses node 


baseclasses = 		 $ \sim$b macro $ \vert$ baseopts classes 


node    = 		 ($ <$Node$ >$ int int int { int }  $ \vert$ $ <$TNode$ >$ int intint { int }) { node }
For the definition of a node ($ <$Node$ >$) in node the first integer is the node number, the second the number of children followed the of children node numbers7.10. The integers in the definition of a terminal node ($ <$TNode$ >$) define the node number, number of base classes associated with the terminal and the base class-index numbers.

Adaptation transforms are defined using 


		  adaptXForm  = 		 $ \sim$a macro adaptOpts $ <$XformSet$ >$ xformset 


adaptOpts   = 		 $ <$AdaptKind$ >$ adaptkind $ <$BaseClass$ >$ baseclasses [$ <$ParentXForm$ >$ parentxform]  


parentxform = 		 $ \sim$a macro $ \vert$ adaptOpts $ <$XformSet$ >$ xformset


adaptKind   = 		 TREE $ \vert$ BASE


xformset    = 		 $ <$XFormKind$ >$ xformKind $ <$NumXForms$ >$ int { linxform }


xformKind   = 		 MLLRMEAN $ \vert$ MLLRCOV $ \vert$ MLLRVAR $ \vert$ CMLLR $ \vert$ SEMIT


linxform    = 		 $ <$LinXForm$ >$ int $ <$VecSize$ >$ int [$ <$OFFSET$ >$ xformbias] 

$ <$BlockInfo$ >$ int int {int} block {block}


xformbias = 		 $ \sim$y macro $ \vert$ $ <$Bias$ >$ short vector 


block       = 		 $ <$Block$ >$ int xform
In the definition of the $ <$BlockInfo$ >$ the first integer is the number of blocks, followed the size of each of the clocks. For examples of the adaptation transform format see section 9.1.5.

Finally the input transform is defined by 


		  inputXform  = 		 $ \sim$j macro $ \vert$ inhead inmatrix


inhead      = 		 $ <$MMFIdMask$ >$ string parmkind [$ <$PreQual$ >$]


inmatrix    = 		 $ <$LinXform$ >$ $ <$VecSize$ >$ int $ <$BlockInfo$ >$ int int {int} block {block}


block       = 		 $ <$Block$ >$ int xform
where the short following $ <$VecSize$ >$ is the number of dimensions after applyingthe linear transform and must match the vector size of the HMM definition. The first short after $ <$BlockInfo$ >$ is the number of block, this is followed by the number of output dimensions from each of the blocks.

Back to HTK site
See front page for HTK Authors