Diffuse reflectance spectroscopy has found many applications in non-invasive monitoring of biological tissues. This technique investigates tissue structure, chromophore concentration, and health by measuring the tissue's optical properties. Commercially available devices typically analyze experimental data using the modified Beer-Lambert's law to determine the relative concentrations of tissue chromophores such as melanin, blood, water, or hemoglobin in arbitrary units. However the tissue scattering coefficient cannot be retrieved. Alternatively, diffuse reflectance data processed with the diffusion approximation can yield absolute chromophore concentration and measure the tissue's scattering coefficient which is related to tissue microstructure. However, this technique requires emitter-detector separation up to 1 cm thus limiting the spatial resolution of these devices. Current spectroscopic techniques are based on the assumption that tissue is homogeneous and that properties are independent of depth. In reality, most bodily organs such as skin, the intestine, or the cervix are protected by a thin lining called the epithelial layer. While the organ is typically composed of connective tissues and perfused with blood vessels and nerves, the protective epithelial layer is bloodless and consists of structured cell layers. Differences in cellular structure and chemical composition give rise to distinct optical properties making the assumption of tissue homogeneity questionable. In skin, for example, the outer epidermal layer is pigmented by melanin which absorbs strongly in the UV while the inner dermal layer is pigmented by blood which absorbs in the visible and near-infrared parts of the spectrum. Furthermore, the thickness of the epidermal layer may vary with anatomical location, gender, and age. The objective of this study is to develop an inverse method based on our semi-empirical model and to assess its robustness in estimating the scattering coefficients, chromophore concentrations in both epidermis and dermis, and the epidermal thickness from spectral diffuse reflectance of human skin.
Approach
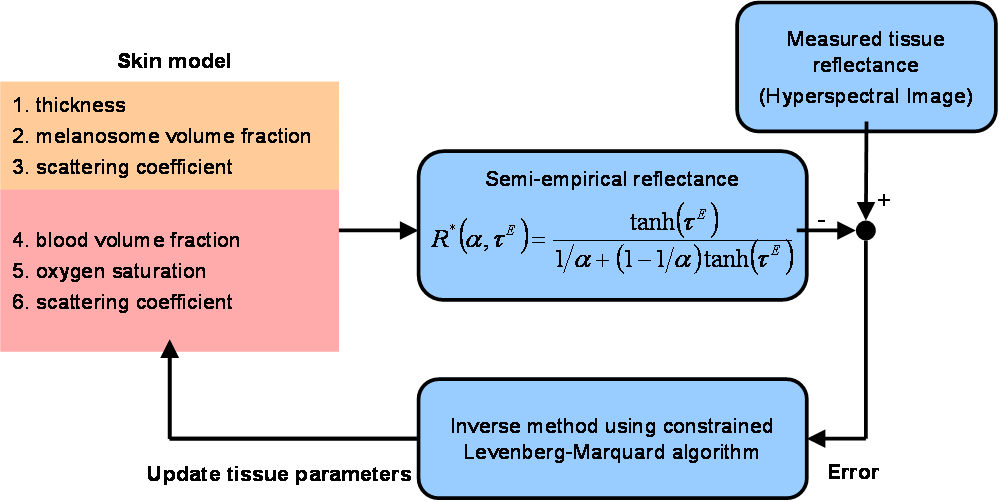
It was assumed that five parameters represented by the property vector ae = [fmel, Lepi, fblood, SO2, b] sufficiently described the biological variability of human skin. The goal of the inverse problem was to estimate the parameter vector ae from the measured diffuse
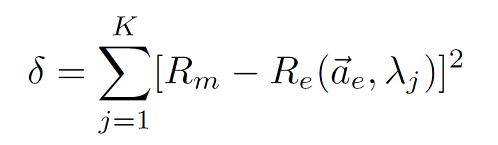
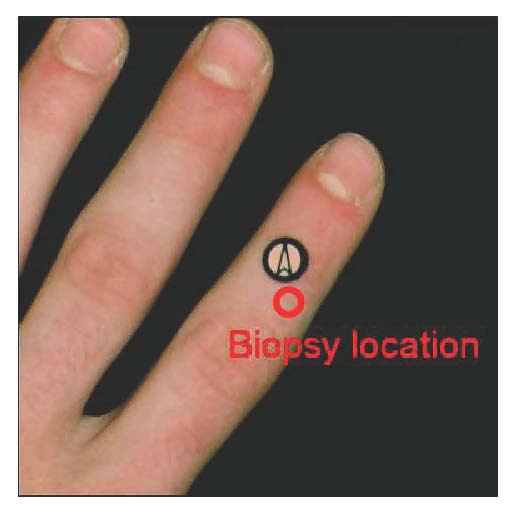
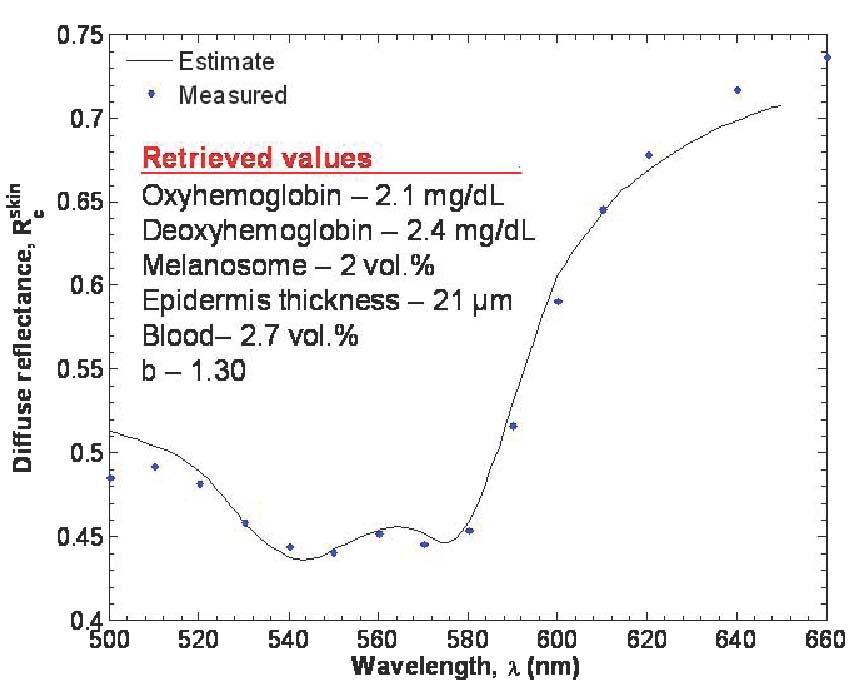
Here is an example of the inverse method applied to a single location of the left hand of a healthy patient
In this study, human skin was modeled as a slab of variable thickness, corresponding to the epidermis, supported by a semi-infinite layer, corresponding to the dermis. Absorption in the epidermis was due to melanin and varied depending on melanosome volume fraction. Absorption in the epidermis was due to oxyhemoglobin and deoxyhemoglobin and varied with blood volume fraction and oxygen saturation. Index of refraction and scattering coefficient in both layers were assumed to be identical. The radiative transfer equation was solved on a spectral basis between 490 and 650 nm by Monte Carlo simulations to produce simulated diffuse reflectance spectra for a wide range of biological properties. Then, an inverse method was used to retrieve physiologically meaningful parameters from the simulated diffuse reflectance spectra. A quicker semi-empirical model [1] was used instead of Monte Carlo simulations in the iterative inversion procedure. The accuracy of the inverse method in estimating fmel, Lepi, SO2, fblood and C was explored for a range of physiologically meaningful values. In summary, all parameters could be estimated with relative rms error less than 5% for fmel between 1 and 8%, Lepi ranging from 20 to 150 microns, SO2 from 25 to 100%, fblood from 1.2 to 10%, and C from 400,000 to 550,000 1/cm. The methodology presented can be applied to any two layer optical system where scattering dominates over absorption.
Publications
D. Yudovsky, A. Nouvong, K. Schomacker, and L. Pilon, 2011. Monitoring Temporal Development and Healing of Diabetic Foot Ulcer Using Hyperspectral Imaging, Journal of Biophotonics, Vol. 4, No. 7-8, pp. 565-576. doi:10.1002/jbio.201000117 pdf
D. Yudovsky and L. Pilon, 2011. Retrieving Skin Properties From In Vivo Diffuse Reflectance Measurements on Human Skin, Journal of Biophotonics, Vol. 4, No.5, pp.305-314, doi:10.1002/jbio.201000069 pdf
D. Yudovsky, A. Nouvong, K. Schomacker, and L. Pilon, 2011. Assessing Diabetic Foot Ulcer Development Risk with Hyperspectral Tissue Oximetry, Journal of Biomedical Optics, Vol.16, No.2, 026009. doi: doi:10.1117/1.3535592 pdf
D. Yudovsky and L. Pilon, 2010. Modeling of Local Excitation Fluence Rate and Florescence Emission in Absorbing and Strongly Scattering Multilayered Media. Applied Optics, Vol. 49, No. 31, pp. 6072-6084. doi:10.1364/AO.49.006072 pdf
D. Yudovsky , A. Nouvong, and L. Pilon, 2010. Hyperspectral Imaging for Diabetic Foot Wound Care, Journal of Diabetes Science and Technology, Vol.4, No.5, pp. 1099-1113. pdf
D. Yudovsky and L. Pilon, 2010. Rapid and Accurate Estimation of Blood Saturation, Melanin Content, and Epidermis Thickness from Spectral Diffuse Reflectance. Applied Optics, Vol. 49, no. 10, pp. 1707-1719. doi:10.1364/AO.49.001707 pdf
D. Yudovsky and L. Pilon, 2009. Simple and Accurate Expressions for Diffuse Reflectance of Semi-Infinite and Two-Layer Absorbing and Scattering Media, Applied Optics, Vol. 48, no. 35, pp. 6670-6683. Selected to appear in The Virtual Journal for Biomedical Optics,Vol. 5, No.1, January 4, 2010. doi:10.1364/AO.48.006670. pdf
L. Pilon, A. Bhowmik, R.-L. Heng, D. Yudovsky, 2015. Simple and Accurate Expressions for Diffuse Reflectance of Semi-Infinite and Two-Layer Absorbing and Scattering Media: Erratum, Applied Optics, Vol. 54, No. 25, pp. 6116-6117. doi: 10.1364/AO.54.006116. pdf (supplementary material: Excel)